题目内容
12.一个不透明的袋子里装有编号分别为1,2,3的球(除编号外,其余都相同),其中1号球1个,3号球1个,从中随机摸出1个球是2号球的概率为$\frac{1}{2}$,设计一个游戏规则:A,B两人同时从袋中摸出一球,两球的和为偶数时A获胜,否则B获胜,试问该游戏是否公平.分析 列表得出所有等可能的情况数,两球的和为偶数的情况数,分别求出两人获胜的概率,比较即可得到游戏公平与否.
解答 解:因为1号球1个,3号球1个,从中随机摸出1个球是2号球的概率为$\frac{1}{2}$,
所以2号球为2个,
所以球带中有四个小球,分别为:1,2,2,3;
列表如下:
| 1 | 2 | 2 | 3 | |
| 1 | (1,1) | (2,1) | (2,1) | (3,1) |
| 2 | (1,2) | (2,2) | (2,2) | (3,2) |
| 2 | (1,2) | (2,2) | (2,2) | (2,3) |
| 3 | (1,3) | (2,3) | (3,2) | (3,3) |
其中两球的和为奇数的情况有8种,概率为$\frac{1}{2}$;
所以该游戏公平.
点评 此题考查了游戏公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
4.果园里有20筐葡萄,每筐以20千克为标准,超过或不足的千克数分别用正、负数来表示,下表记录了这20筐葡萄超过或不足20千克的情况:
(1)20筐葡萄中,最重的一筐比最轻的一筐重5.5千克.
(2)这20筐葡萄的总质量多少千克?
(3)若葡萄每千克售价8元,则售完这20筐葡萄一共可收入多少元?
| 单位(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 5 | 2 | 2 | 4 | 6 |
(2)这20筐葡萄的总质量多少千克?
(3)若葡萄每千克售价8元,则售完这20筐葡萄一共可收入多少元?
 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.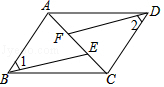 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠1=∠2,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠1=∠2,AF=CE.