题目内容
阅读材料,解答下列各题:
例:当a,b实数时,则a2+b2≥2ab,(当且仅当a=b时,等号成立).因为(a-b)2≥0,即a2-2ab+b2≥0所以a2+b2≥2ab.
(1)请仿照例中的方法,证明当a,b为非负数时,a+b≥2
;
(2)已知a>0,求2a+
的最小值.
例:当a,b实数时,则a2+b2≥2ab,(当且仅当a=b时,等号成立).因为(a-b)2≥0,即a2-2ab+b2≥0所以a2+b2≥2ab.
(1)请仿照例中的方法,证明当a,b为非负数时,a+b≥2
| ab |
(2)已知a>0,求2a+
| 2 |
| a |
考点:完全平方公式
专题:阅读型
分析:(1)根据阅读材料中的例证,得出(
-
)2≥0,进一步证明得出结论即可;
(2)利用(1)的结论进一步计算得出结果即可.
| a |
| b |
(2)利用(1)的结论进一步计算得出结果即可.
解答:解:(1)∵(
-
)2≥0(a,b为非负数)
即a-2
+b≥0
∴a+b≥2
;
(2)∵a>0,
∴(2a-
)2≥0
∴(2a+
)2≥4×2a×
∴2a+
≥4
∴2a+
的最小值是4.
| a |
| b |
即a-2
| ab |
∴a+b≥2
| ab |
(2)∵a>0,
∴(2a-
| 2 |
| a |
∴(2a+
| 2 |
| a |
| 2 |
| a |
∴2a+
| 2 |
| a |
∴2a+
| 2 |
| a |
点评:此题考查利用完全平方公式证明几何不等式的成立以及简单的运用.

练习册系列答案
相关题目
下列算式能用平方差公式计算的是( )
| A、(-a+b)(a-b) |
| B、(x+2)(2+x) |
| C、(x-y)(-x-y) |
| D、(x-2)(x+1) |
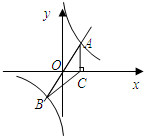 如图,直线y=x与反比例函数
如图,直线y=x与反比例函数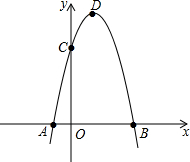 如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D 如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,BC=5,CF=3,BF=4.求证:DE∥FC.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,BC=5,CF=3,BF=4.求证:DE∥FC.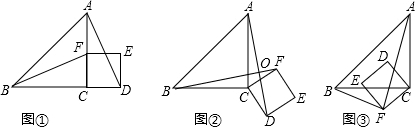
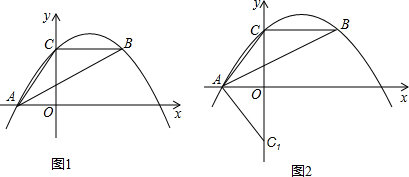
 如图,四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=
如图,四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=