题目内容
 如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长.
如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长.考点:翻折变换(折叠问题)
专题:
分析:根据图形折叠前后图形不发生大小变化可得出∠CBE=∠CBE,再证明△FMG≌△BCE,然后利用勾股定理的知识求出GF的长.
解答: 解:作FM⊥BC,垂足为M,连接EF,
解:作FM⊥BC,垂足为M,连接EF,
∵将正方形纸片ABCD折叠,使得点B落在边CD上的E点,折痕为GF,
∴∠C=∠BNG=90°,∠CBE=∠CBE,
∴△BNG∽△BCE,
∴∠BGN=∠BEC,
在△FMG与△BCE中,
,
∴△FMG≌△BCE(AAS),
∴MG=CE=5,
又∵在Rt△MFG中,FM=12,
∴根据勾股定理得:FG=
=13.
故GF的长是13.
 解:作FM⊥BC,垂足为M,连接EF,
解:作FM⊥BC,垂足为M,连接EF,∵将正方形纸片ABCD折叠,使得点B落在边CD上的E点,折痕为GF,
∴∠C=∠BNG=90°,∠CBE=∠CBE,
∴△BNG∽△BCE,
∴∠BGN=∠BEC,
在△FMG与△BCE中,
|
∴△FMG≌△BCE(AAS),
∴MG=CE=5,
又∵在Rt△MFG中,FM=12,
∴根据勾股定理得:FG=
| FM2+MG2 |
故GF的长是13.
点评:此题主要考查了图形的翻折变换,根据图形折叠前后图形不发生大小变化得出三角形的全等是解决问题的关键,难度一般.

练习册系列答案
相关题目
已知方程组
有无数多个解,则a、b的值等于( )
|
| A、a=-3,b=-14 |
| B、a=3,b=-7 |
| C、a=-1,b=9 |
| D、a=-3,b=14 |
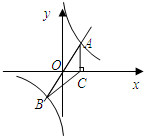 如图,直线y=x与反比例函数
如图,直线y=x与反比例函数
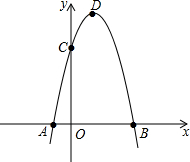 如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D 如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,BC=5,CF=3,BF=4.求证:DE∥FC.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,BC=5,CF=3,BF=4.求证:DE∥FC.