题目内容
 如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°,
如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°,(1)求证:△ABC是等边三角形;
(2)若AC=2
| 3 |
考点:圆周角定理,等边三角形的判定与性质
专题:
分析:(1)若要证明△ABC是等边三角形,则只要证明∠A=∠ACB=∠ABC=60°即可;
(2)根据AC的长,可以求出圆的半径,进而可求出⊙O的周长.
(2)根据AC的长,可以求出圆的半径,进而可求出⊙O的周长.
解答:(1)证明:∵∠ACB=∠BDC=60°,
∴∠A=60°,
∴∠ABC=60°,
∴△ABC是等边三角形;
(2)解:∵△ABC是等边三角形,
∴∠BOC=120°,
∵AC=2
,
∴BC=2
,
∴BO=2,
∴⊙O的周长是4π.
∴∠A=60°,
∴∠ABC=60°,
∴△ABC是等边三角形;
(2)解:∵△ABC是等边三角形,
∴∠BOC=120°,
∵AC=2
| 3 |
∴BC=2
| 3 |
∴BO=2,
∴⊙O的周长是4π.
点评:本题考查了圆周角定理、等边三角形的判定和性质以及圆的周长公式的运用,题目比较简单,是中考常见题型.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得∠ADE=30°,量出DC=2m,BC=30m,请帮助小明计算出树高AB.
如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得∠ADE=30°,量出DC=2m,BC=30m,请帮助小明计算出树高AB.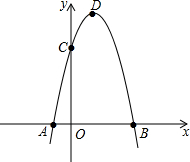 如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
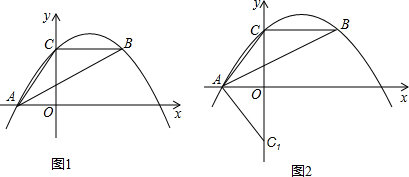
如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D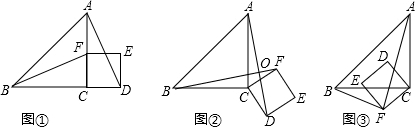
 如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.
如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.