题目内容
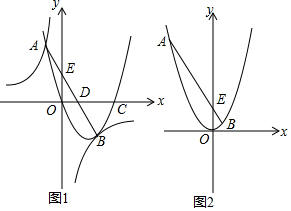
2.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y=$\frac{k}{x}$相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(-1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)先根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,再用待定系数法求出抛物线的解析式;
(2)先求出直线AB的解析式,进而求出点D的坐标,最后用三角形的面积和求解即可;
(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.
解答 解:(1)把点A的坐标代入双曲线的解析式得:k=-1×4=-4.
所以双曲线的解析式为y=-$\frac{4}{x}$.
设点B的坐标为(m,-m).
∵点B在双曲线上,
∴-m2=-4,解得m=2或m=-2.
∵点B在第四象限,
∴m=2.
∴B(2,-2).
将点A、B、C的坐标代入得:$\left\{\begin{array}{l}{a-b+c=4}\\{4a+2b+c=-2}\\{c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-3}\\{c=0}\end{array}\right.$.
∴抛物线的解析式为y=x2-3x.
(2)如图1, 连接AC、BC.
连接AC、BC.
令y=0,则x2-3x=0,
∴x=0或x=3,
∴C(3,0),
∵A(-1,4),B(2,-2),
∴直线AB的解析式为y=-2x+2,
∵点D是直线AB与x轴的交点,
∴D(1,0),
∴S△ABC=S△ADC+S△BDC=$\frac{1}{2}$×2×4+$\frac{1}{2}$×2×2=6;
(3)存在,理由:如图2,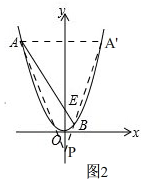 由原抛物线的解析式为y=x2-3x=(x-$\frac{3}{2}$)2-$\frac{9}{4}$,
由原抛物线的解析式为y=x2-3x=(x-$\frac{3}{2}$)2-$\frac{9}{4}$,
∴原抛物线的顶点坐标为($\frac{3}{2}$,-$\frac{9}{4}$),
∴抛物线向左平移$\frac{3}{2}$个单位,再向上平移$\frac{9}{4}$个单位,
而平移前A(-1,4),B(2,-2),
∴平移后点A(-$\frac{5}{2}$,$\frac{25}{4}$),B($\frac{1}{2}$,$\frac{1}{4}$),
∴点A关于y轴的对称点A'($\frac{5}{2}$,$\frac{25}{4}$),
连接A'B并延长交y轴于点P,连接AP,
由对称性知,∠APE=∠BPE,
∴△APB的内切圆的圆心在y轴上,
∵B($\frac{1}{2}$,$\frac{1}{4}$),A'($\frac{5}{2}$,$\frac{25}{4}$),
∴直线A'B的解析式为y=3x-$\frac{5}{4}$,
∴P(0,-$\frac{5}{4}$).
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积公式,对称的性质,解(1)的关键是求出点B的坐标,解(2)的关键是求出点D的坐标,解(3)的关键是确定出点A关于y轴的对称点A'的坐标,是一道基础题目.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【思考】
(1)根据所给条件,完成下表:
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
【探究】
(3)该公司所建房资金不少于5700万元,且所筹资金全部用于建房,若A户型不超过32套,则该公司有哪几种建房方案?
(4)在(3)的前提下,根据国家房地产政策,公司计划每套A户型住房的售价降低a万元(0<a≤3),B户型住房的售价不变,且预计所建的两种住房全部售出,求该公司获得最大利润的方案.
【决策】
为了适应市场需要,该公司在总套数不变的情况下,改建若干套C户型,现已知C户型每套成本110万元,售价118万元.若该公司所筹资金为6300万元且刚好用完,则当x=45套时,该公司所建房售出后获得的总利润最大.
| 手机型号 | A型 | B型 |
| 进价(单位:元/部) | 900 | 1200 |
| 预售价(单位:元/部) | 1200 | 1600 |
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
②求出预估利润的最大值,并写出此时购进两款手机各多少部.
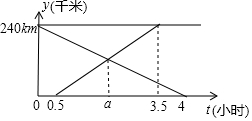 甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.
甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.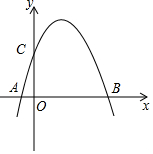 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.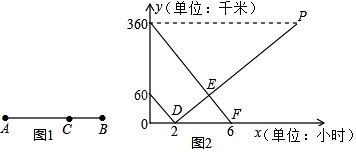
 如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:
如图,分别表示甲步行与乙汽自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题: