题目内容
13.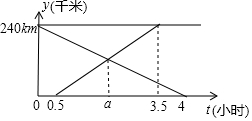 甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.
甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.(1)a=2;
(2)若甲乙两车之间的距离s(米),则s与甲车出发时间t≥a之间的函数关系式为:s=$\left\{\begin{array}{l}{140t-280(2≤t≤3.5)}\\{60t(3.5<t≤4)}\end{array}\right.$.
分析 (1)根据速度=路程÷时间,分别求出甲、乙两车的速度,再根据二者相遇的时间=甲先出发0.5小时后两车的距离÷两车速度和,即可求出a值;
(2)分2≤t≤3.5和3.5<t≤4两种情况考虑,当2≤t≤3.5时,根据两车之间距离=两车速度和×两车相遇后又行驶的时间,即可找出s与t之间的函数关系式;当3.5<t≤4时,根据两车之间的距离=210+甲车的速度×乙车到达终点后甲车又行驶的时间,即可找出s与t之间的函数关系式.综上即可得出结论.
解答 解:(1)甲车的速度为240÷4=60(千米/小时),
乙车的速度为240÷(3.5-0.5)=80(千米/小时),
二者相遇的时间a=(240-60×0.5)÷(60+80)+0.5=2(小时).
故答案为:2.
(2)当2≤t≤3.5时,s=(60+80)×(t-2)=140t-280;
当3.5<t≤4时,s=(60+80)×(3.5-2)+60(t-3.5)=60t.
综上所述:甲乙两车之间的距离s与甲车出发时间t≥a之间的函数关系式为s=$\left\{\begin{array}{l}{140t-280(2≤t≤3.5)}\\{60t(3.5<t≤4)}\end{array}\right.$.
故答案为:s=$\left\{\begin{array}{l}{140t-280(2≤t≤3.5)}\\{60t(3.5<t≤4)}\end{array}\right.$.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据数量关系,列式计算;(2)分2≤t≤3.5和3.5<t≤4两种情况,根据数量关系找出s与t之间的函数关系式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
8.下列调查中,适合用全面调查方式的是( )
| A. | 了解我市上班族的收入情况 | |
| B. | 了解全市市民的身高情况 | |
| C. | 了解某班学生期末考数学科成绩情况 | |
| D. | 了解我市的空气污染情况 |
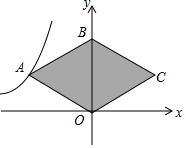 如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.
如图,O是坐标原点,菱形OABC的顶点B的坐标为(0,4),反比例函数y=-$\frac{8}{x}$(x<0)的图象经过点A,则菱形OABC的面积为16.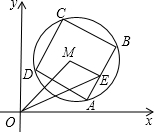 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.