题目内容
17.如图1所示,在A,B两地之间有汽车站C站(AC>BC),客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.求: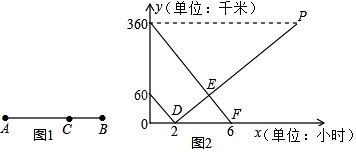
(1)A,B两地的距离;
(2)在图2中点P的坐标.
分析 (1)根据时间为0时,客车和货车距离C站的距离即可解题;
(2)根据AB距离和货车行驶速度,即可求得点P的横坐标,即可解题.
解答 解:(1)当t=0时,
客车距C站360千米,货车距C站60千米,
∴A,B两地的距离=60千米+360千米=420千米;
(2)由图2可得货车行驶2小时后到达C站,
即货车速度为60÷2=30(千米/小时),
∴货车到达A站需要420÷30=14(小时),
∴图2中点P坐标为(14,360).
答:A,B两地的距离为420千米,图2中点P的坐标为(14,360).
点评 此题为一次函数的应用,读懂图中给出的信息是解题的关键.

练习册系列答案
相关题目
7. 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )| A. | 12π | B. | 15π | C. | 24π | D. | 30π |
 已知抛物线y=x2-3kx+2k+4
已知抛物线y=x2-3kx+2k+4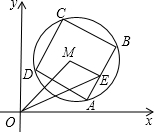 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.