题目内容
8.对任意有理数x,y定义新运算“⊕”如下:x⊕y=x2-y,若|a-3|+(b+2)2=0,则a⊕b=( )| A. | 5 | B. | 1 | C. | 11 | D. | 7 |
分析 利用非负数的性质求出a与b的值,再利用新定义计算即可求出所求式子的值.
解答 解:∵|a-3|+(b+2)2=0,
∴a-3=0,b+2=0,
解得:a=3,b=-2,
则原式=9+2=11,
故选C
点评 此题考查了有理数的混合运算,以及非负数的性质:绝对值与偶次幂,弄清题中的新定义是解本题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
16.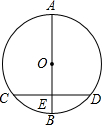 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
20.已知△ABC是等边三角形,则cos2A的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
17.下列运算中正确的是( )
| A. | a3+a3=2a6 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a2÷a5=a-3 |
 如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.
如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.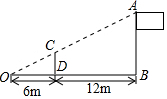 如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.
如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m. 如图点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,CD=6,求线段AB的长.
如图点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,CD=6,求线段AB的长.