题目内容
19.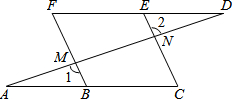 如图,已知,∠1=∠2,∠A=∠D,对∠C=∠F说明理由.
如图,已知,∠1=∠2,∠A=∠D,对∠C=∠F说明理由.理由:∵∠A=∠D(已知)
∴AC∥FD内错角相等,两直线平行
∴∠C=∠DEC两直线平行,内错角相等
又∵∠1=∠DMF对顶角相等
∠1=∠2(已知)
∴∠DMF=∠2等量代换
∴EC∥BF同位角相等,两直线平行
∴∠DEC=∠F两直线平行,同位角相等
∴∠C=∠F.
分析 由内错角相等两直线平行,填第一个空;由两直线平行内错角相等,填第二个空;由对顶角相等,填第三个空;根据等量代换填第四个空;由同位角相等两直线平行,填第五个空;由两直线平行同位角相等,填第六个空.
解答 解:理由:∵∠A=∠D(已知)
∴AC∥FD (内错角相等,两直线平行),
∴∠C=∠DEC( 两直线平行,内错角相等),
∵∠1=∠DMF(对顶角相等),
∠1=∠2(已知),
∴∠DMF=∠2(等量代换),
∴EC∥BF ( 同位角相等,两直线平行),
∴∠DEC=∠F (两直线平行,同位角相等),
∴∠C=∠F.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
9.为了了解我市15000名学生的视力情况,抽查了解1000名学生的视力进行统计分析,下列四个判断正确的是( )
| A. | 15000名学生是总体 | |
| B. | 样本容量是1000名 | |
| C. | 每名学生是总体的一个样本 | |
| D. | 1000名学生的视力是总体的一个样本 |
7.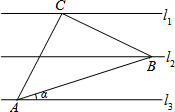 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的直角顶点C在l1上,另两个顶点A、B分别在l2、l3上,则tanα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
4.多项式x2-x-12可以因式分解成( )
| A. | (x+3)(x+4) | B. | (x-3)(x+4) | C. | (x+3)(x-4) | D. | (x-3)(x-4) |
8.如果把$\frac{5x}{x+y}$中的x与y都扩大为原来的5倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 缩小为原来的$\frac{1}{5}$ | D. | 扩大为原来的10倍 |
9. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=125°,则∠3等于( )| A. | 15° | B. | 25° | C. | 35° | D. | 45° |
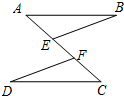 如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.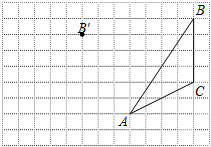 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: