题目内容
17.如图,在平面直角坐标系中,四边形OABC是边长为2的菱形,且∠AOC=60°.(1)求经过O,A,C三点的抛物线的表达式.
(2)记(1)中抛物线为L,若将菱形OABC绕点O旋转60°,得到新的菱形OA′B′C′,记经过点A′,B′,C′三点的抛物线为L′,L′可由L平移得到吗?若可以,请写出平移方式:若不可以,请说明理由.
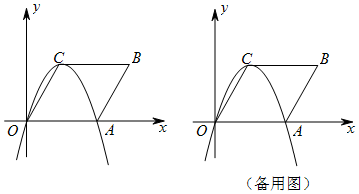
分析 (1)先确定出点C的坐标利用待定系数法求出抛物线L的解析式;
(2)先将菱形旋转后确定出点A',B',C,利用待定系数法确定出抛物线L'的解析式,即可.
解答 解:(1)如图1,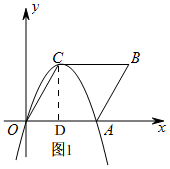 ∵四边形OABC是菱形,
∵四边形OABC是菱形,
∴OC=OA=AB=2,
∴A(2,0)
过点C作CD⊥OA于D,
在Rt△OCD中,∠AOC=60°,OC=2,
∴OD=1,CD=$\sqrt{3}$,
∴C(1,$\sqrt{3}$,),
设过点O,A,C的抛物线为L的解析式为y=a(x-2),
∴$\sqrt{3}$=a(1-2),
∴a=-$\sqrt{3}$,
∴抛物线L的解析式为y=-$\sqrt{3}$x(x-2)=-$\sqrt{3}$(x-1)2+$\sqrt{3}$=-$\sqrt{3}$x2+2$\sqrt{3}$x
(2)可以,理由:如图2,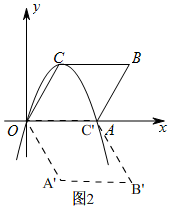
将菱形OABC绕点O旋转60°,得到新的菱形OA′B′C′,
∴点C'和点A重合,
∴C'(2,0),
易知,A'(1,-$\sqrt{3}$),B'(3,-$\sqrt{3}$),
设过点A',B',C'的抛物线L'的解析式为y=a'x2+bx+c,
∴$\left\{\begin{array}{l}{a'+b+c=-\sqrt{3}}\\{9a'+3b+c=-\sqrt{3}}\\{4a'+2b+c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a'=-\sqrt{3}}\\{b=4\sqrt{3}}\\{c=-4\sqrt{3}}\end{array}\right.$,
∴过点A',B',C'的抛物线L'的解析式为y=-$\sqrt{3}$x2+4$\sqrt{3}$x-4$\sqrt{3}$=-$\sqrt{3}$(x-2)2,
∵抛物线L和L'的二次系数一样,都是-$\sqrt{3}$,
∴抛物线L'是抛物线L向下平移$\sqrt{3}$单位,再向右平移1个单位.
点评 此题是二次函数综合题,主要考查了待定系数法,菱形的性质,旋转的性质,平移的性质,解(1)的关键是确定出点C的坐标,解(2)的关键是确定出过点A',B',C'的抛物线的解析式.

 阅读快车系列答案
阅读快车系列答案| A. | k≠0 | B. | k为一切实数 | C. | k≥-$\frac{1}{2}$且k≠0 | D. | k≥-$\frac{1}{2}$ |
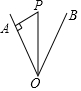 如图,点P在∠AOB的平分线上,PA⊥OA于A,若PA=3,则点P到OB的距离为( )
如图,点P在∠AOB的平分线上,PA⊥OA于A,若PA=3,则点P到OB的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.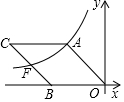 如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.
如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.