题目内容
2.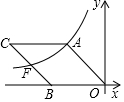 如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.
如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.
分析 过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF=$\frac{1}{2}$S菱形OBCA,结合菱形的面积公式即可得出结论.
解答 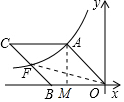 解:过点A作AM⊥x轴于点M,连接OF,如图所示.
解:过点A作AM⊥x轴于点M,连接OF,如图所示.
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=$\frac{4}{5}$,
∴AM=OA•sin∠AOB=$\frac{4}{5}$a,
∴点A的坐标为($\frac{3}{5}$a,$\frac{4}{5}$a).
∵四边形OACB是菱形,点F在边BC上,
∴S△AOF=$\frac{1}{2}$S菱形OBCA=$\frac{1}{2}$OB•AM=$\frac{1}{2}$•a•$\frac{4}{5}$a=20,
解得a2=50,
∴k=$\frac{3}{5}$a×$\frac{4}{5}$a=$\frac{12}{25}$×50=24,
则该反比例函数的表达式为y=$\frac{24}{x}$.
故答案是:y=$\frac{24}{x}$.
点评 本题考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出S△AOF=$\frac{1}{2}$S菱形OBCA.

练习册系列答案
相关题目
10.一元二次方程x2-5x+2=0的两根为a,b时,则a+b-ab的值是( )
| A. | 7 | B. | 3 | C. | -3 | D. | -7 |
11.将抛物线y=x2向右平移3个单位,再向下平移2个单位后所得抛物线的表达式为( )
| A. | y=(x+3)2-2 | B. | y=(x-3)2-2 | C. | y=(x+2)2-3 | D. | y=(x-2)2-3 |
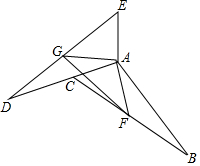 如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.
如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.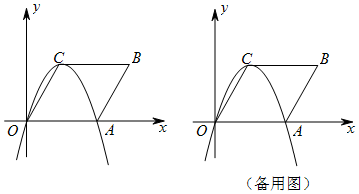
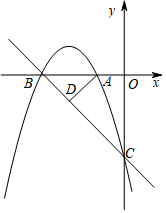 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(-3,0)两点,与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(-3,0)两点,与y轴交于点C.