题目内容
7．关于x的方程kx2+（1-k）x-1=0有实数根，则k的取值范围是（ ）| A． | k≠0 | B． | k为一切实数 | C． | k≥-$\frac{1}{2}$且k≠0 | D． | k≥-$\frac{1}{2}$ |
分析 根据判别式的作用即可求出答案．
解答 解：当k=0时，
此时方程为：x-1=0，满足题意．
当k≠0时，
由题意可知：△=（1-k）2+4k
=1-2k+k2+4k
=（k+1）2≥0，
∴k为任意实数，
故答案为：（B）
点评 本题考查根的判别式，解题的关键是正确理解运用判别式的作用，本题属于基础题型．
练习册系列答案
相关题目
如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
如图，边长为2的菱形ABCD的两个顶点A、B分别在x轴、y轴上运动，C、D在第一象限，∠BCD=120°，则OD的最大值是（ ）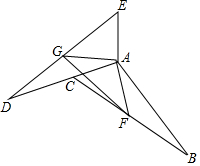
如图，把△ABC绕点A顺时针旋转n度（0＜n＜180）后得到△ADE，并使点D落在AC的延长线上．