题目内容
6.先化简,再求值:$\frac{1-a}{{a}^{2}+a}$÷($\frac{1-a}{a}$-a+1),其中,a=$\sqrt{2}$-1.分析 首先化简$\frac{1-a}{{a}^{2}+a}$÷($\frac{1-a}{a}$-a+1),然后把a=$\sqrt{2}$-1代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{1-a}{{a}^{2}+a}$÷($\frac{1-a}{a}$-a+1)
=$\frac{1-a}{a(1+a)}$÷$\frac{(1-a)(1+a)}{a}$
=$\frac{1}{{(1+a)}^{2}}$
当a=$\sqrt{2}$-1时,
原式=$\frac{1}{{(1+\sqrt{2}-1)}^{2}}$=$\frac{1}{2}$
点评 此题主要考查了分式的化简求值问题,要熟练掌握,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
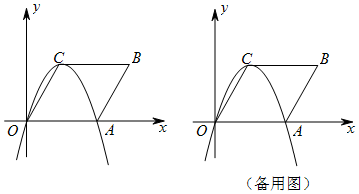
11.将抛物线y=x2向右平移3个单位,再向下平移2个单位后所得抛物线的表达式为( )
| A. | y=(x+3)2-2 | B. | y=(x-3)2-2 | C. | y=(x+2)2-3 | D. | y=(x-2)2-3 |
18.已知函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
| A. | k<4且k≠3 | B. | k≤4且k≠3 | C. | k<4 | D. | k≤4 |
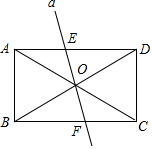 在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,
在矩形ABCD中,AC,BD交于点O,直线α经过点O,且α⊥BD交AD于E点,交BC于F点,