题目内容
4.已知抛物线y=ax2+bx+c(a>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为点D.且OB=OC=3OA,点B(3,0).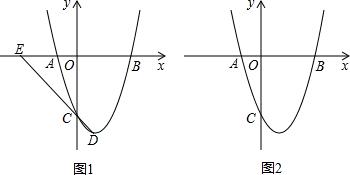
(1)求抛物线的解析式.
(2)如图1,直线CD与x轴交于点E,直线l∥DE且交抛物线于M、N两点,若以点D、E、M、N为顶点的四边形为平行四边形,求直线l的解析式.
(3)如图2,若平行于x轴的直线与抛物线交于P、Q两点,且以PQ为直径的圆与x轴相切,求该圆半径的长.
分析 (1)由OB=OC=3OA,结合点B坐标可得出点A的坐标,再有a>0可得出点C在y轴负半轴上,进而得出点C的坐标,根据点A、B、C的坐标利用待定系数法即可求出抛物线解析式;
(2)根据抛物线的解析式找出点D的坐标,利用待定系数法找出直线CD的解析式,根据一次函数图象上点的坐标特征找出点E的坐标,根据直线ll∥DE,可设出直线l的解析式,将其代入抛物线解析式中根据根与系数的关系可找出点M、N横坐标之间的关系,再结合平行四边形的性质以及点D、E的坐标即可得出关于n的方程,解方程即可求出n值,进而得出直线l的解析式;
(3)令线段PQ的中点为E,⊙E与x轴的切点为点F,连接EF,设直线PQ的解析式为y=m,将其代入抛物线解析式中根据根与系数的关系可找出点P、Q横坐标之间的关系,再根据切线的性质即可得出关于m的方程,解方程求出m值,取m的绝对值即可得出结论.
解答 解:(1)∵OB=OC=3OA,点B(3,0),a>0,
∴A(-1,0),抛物线与y轴的交点在负半轴,
∴C(0,-3),
将A(-1,0)、B(3,0)、C(0,-3)代入y=ax2+bx+c中,
∴$\left\{\begin{array}{l}{0=a-b+c}\\{0=9a+3b+c}\\{-3=c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$,
∴抛物线的解析式为y=x2-2x-3.
(2)∵y=x2-2x-3=(x-1)2-4,
∴D(1,-4).
设直线CD的解析式为y=kx-3,则有-4=k-3,
解得:k=-1,
∴直线CD的解析式为y=-x-3.
当y=0时,有0=-x-3,解得:x=-3,
∴E(-3,0).
∵直线l∥DE,
∴设直线l的解析式为y=-x+n,
将y=-x+n代入y=x2-2x-3中,整理得:x2-x-(3+n)=0,
∴xM+xN=1,xM•xN=-(3+n),
∵以点D、E、M、N为顶点的四边形为平行四边形,且DE∥MN,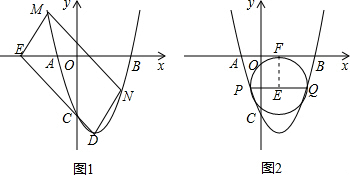
∴|xM-xN|=$\sqrt{({x}_{M}+{x}_{N})^{2}-4{x}_{M}•{x}_{N}}$=$\sqrt{13+4n}$=1-(-3)=4,
解得:n=$\frac{3}{4}$,
∴直线l的解析式为y=-x+$\frac{3}{4}$.
(3)令线段PQ的中点为E,⊙E与x轴的切点为点F,连接EF,如图所示.
∵PQ∥x轴,抛物线的顶点D(1,-4),
∴设直线PQ的解析式为y=m,则E(1,m),F(1,0).
将y=m代入y=x2-2x-3中,整理得:x2-2x-(3+m)=0,
∴xP+xQ=2,xP•xQ=-(3+m),
∵PQ=2EF,
∴|xP-xQ|=$\sqrt{({x}_{P}+{x}_{Q})^{2}-4{x}_{P}•{x}_{Q}}$=$\sqrt{16+4m}$=2|m|,
解得:m=$\frac{1±\sqrt{17}}{2}$.
∴该圆半径的长为$\frac{1+\sqrt{17}}{2}$或$\frac{\sqrt{17}-1}{2}$.
点评 本题考查了待定系数法求函数解析式、根与系数的关系以及切线的性质,解题的关键是:(1)利用待定系数法求出函数解析式;(2)找出关于n的方程;(3)找出关于m的方程.本题属于中档题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

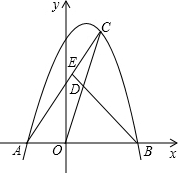 如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
 如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现要在此区域内建一图书馆P,使它到两条道路的距离相等,并且到两所学校的距离也相等,求P点位置.(不写作法,保留作图痕迹)
如图所示,在道路OA、OB的交叉区域内有M、N两所学校,现要在此区域内建一图书馆P,使它到两条道路的距离相等,并且到两所学校的距离也相等,求P点位置.(不写作法,保留作图痕迹) 如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,
如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,
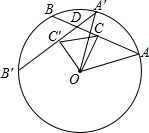 如图,在⊙O中.AB弧的度数为100,把弦AB绕圆心旋转60,得到线段A′B′,交AB于D,作OC⊥AB,OC′⊥A′B′,C,C′分别为垂足,连结CC′.
如图,在⊙O中.AB弧的度数为100,把弦AB绕圆心旋转60,得到线段A′B′,交AB于D,作OC⊥AB,OC′⊥A′B′,C,C′分别为垂足,连结CC′.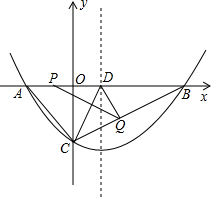 已知:抛物线y=$\frac{1}{16}$x2+bx+c(c<0)的图象与x轴的负半轴相较于点A,与x轴的正半轴相交于点B,与y轴交与点C,8OC2=3OA•OB且△ABC的面积为60.
已知:抛物线y=$\frac{1}{16}$x2+bx+c(c<0)的图象与x轴的负半轴相较于点A,与x轴的正半轴相交于点B,与y轴交与点C,8OC2=3OA•OB且△ABC的面积为60.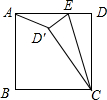 如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.
如图,正方形ABCD中,AB=4,E是边AD上一点,将△EDC沿EC翻折,点D的对应点D′落在正方形内部,若△AD′E恰是以D′E为腰的等腰三角形,那么DE的长为4$\sqrt{2}$-4或2.