题目内容
12. 如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,
如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,求证:AE•AB=AF•AC.
分析 证明△ABD∽△ADE,得出对应边成比例$\frac{AD}{AE}=\frac{AB}{AD}$,得出AD2=AE•AB,同理:AD2=AF•AC,即可得出结论.
解答 证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵DE⊥AB,
∴△ABD∽△ADE,
∴$\frac{AD}{AE}=\frac{AB}{AD}$,
∴AD2=AE•AB,
同理:AD2=AF•AC,
∴AE•AB=AF•AC.
点评 本题考查相似三角形的判定与性质;证明三角形相似得出对应边成比例是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | 3-x>3-y | C. | -2x<-2y | D. | x+3>y-3 |
18.下列性质中,菱形具有而平行四边形不具有的性质是( )
| A. | 对边平行且相等 | B. | 对角线互相平分 | C. | 对角线互相垂直 | D. | 对角互补 |
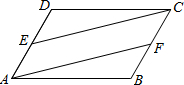 如图,已知E、F分别是边AD、BC的中点,AD=BC,AD∥BC,则AF=CE,试说明理由.
如图,已知E、F分别是边AD、BC的中点,AD=BC,AD∥BC,则AF=CE,试说明理由.