Question

9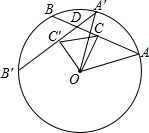．如图，在⊙O中．AB弧的度数为100，把弦AB绕圆心旋转60，得到线段A′B′，交AB于D，作OC⊥AB，OC′⊥A′B′，C，C′分别为垂足，连结CC′．
（1）求证：∠OCC′=∠OC′C；
（2）求证：Rt△AOC全等于Rt△A′OC′，
（3）求∠ADA′的度数和弧A′B的度数．

Answer 1

分析 （1）只要证明OC=OC′，即可解决问题．
（2）根据斜边直角边对应相等的两个三角形全等即可证明．
（3）首先求出AA′弧的度数为60°，A′B弧的度数为40°，再根据∠A′DA=∠DBA′+∠BA′B′，证明∠ABA′=∠BA′B′=30°即可解决问题．

解答 解：（1）∵OC⊥AB，OC′⊥A′B′，
∴AC=BC，A′C′=′B′C，
∵AB=A′B′，
∴AC=A′C′，
在Rt△AOC和Rt△A′OC′中，$\left\{\begin{array}{l}{OA=OA′}\\{AC=A′C′}\end{array}\right.$，
∴△AOC≌△A′OC′，
∴OC=OC′，
∴∠OCC′=∠OC′C．

（2）∵OC⊥AB，OC′⊥A′B′，
∴AC=BC，A′C′=′B′C，
∵AB=A′B′，
∴AC=A′C′，
在Rt△AOC和Rt△A′OC′中，
$\left\{\begin{array}{l}{OA=OA′}\\{AC=A′C′}\end{array}\right.$，
∴△AOC≌△A′OC′．

（3）∵AB弧的度数为100°，∠AOA′=60°，
∴AA′弧的度数为60°，A′B弧的度数为40°，
∵AB弧=A′B′弧，
∴BB′弧=AA′弧，
∴BB′弧的度数为60°，
∴∠ABA′=∠BA′B′=30°
∴∠A′DA=∠DBA′+∠BA′B′=60°，
∴∠A′DA=60°，A′B弧的度数为40°．

点评 本题考查圆综合题、全等三角形的判定和性质、等腰三角形的判定和性质，圆周角的度数与所对的弧的度数之间的关系等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．