题目内容
10.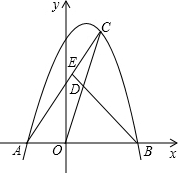 如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
分析 过点O作OH∥AC交BE于点H,根据A、B的坐标可得OA=m,OB=2m,AB=3m,证明OH=CE,将根据$\frac{CE}{AE}$=$\frac{OH}{AE}$=$\frac{OB}{AB}$,可得出答案.
解答 解: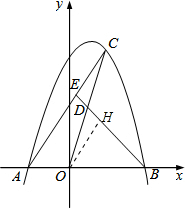 过点O作OH∥AC交BE于点H,
过点O作OH∥AC交BE于点H,
令y=-x2+mx+2m2=0,
∴x1=-m,x2=2m,
∴A(-m,0)、B(2m,0),
∴OA=m,OB=2m,AB=3m,
∵D是OC的中点,
∴CD=OD,
∵OH∥AC,
∴$\frac{OH}{CE}$=$\frac{OD}{CD}$=1,
∴OH=CE,
∴$\frac{CE}{AE}$=$\frac{OH}{AE}$=$\frac{BO}{AB}$,
∴$\frac{CE}{AE}$=$\frac{2m}{3m}$=$\frac{2}{3}$,
故选D.
点评 本题主要考查了抛物线与x轴的交点问题,解题的关键是过点O作OH∥AC交BE于点H,此题有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列方程中,是一元二次方程的是( )
| A. | 3x+7=0 | B. | x2+5x=-6 | C. | x(x+5)=x3-1 | D. | 3x2-$\frac{7}{x}$=0 |
18.下列性质中,菱形具有而平行四边形不具有的性质是( )
| A. | 对边平行且相等 | B. | 对角线互相平分 | C. | 对角线互相垂直 | D. | 对角互补 |
5.下列方程是一元二次方程的是( )
| A. | 2x+y=0 | B. | x-4=5x | C. | x2-3x=6 | D. | x+$\frac{4}{x}$=1 |
15.近似数3.70所表示的准确值x的取值范围是( )
| A. | 3.695≤x<3.705 | B. | 3.60<x<3.80 | C. | 3.695<x≤3.705 | D. | 3.700<x≤3.705 |