题目内容
3. 如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,如果AB=9,BD=3,那么CF的长度为2.
如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,如果AB=9,BD=3,那么CF的长度为2.
分析 利用两对相似三角形,线段成比例:AB:BD=AE:EF,CD:CF=AE:EF,可得CF=2.
解答 解:如图,∵△ABC和△ADE均为等边三角形,
∴∠B=∠BAC=60°,∠E=∠EAD=60°,
∴∠B=∠E,∠BAD=∠EAF,
∴△ABD∽△AEF,
∴AB:BD=AE:EF.
同理:△CDF∽△EAF,
∴CD:CF=AE:EF,
∴AB:BD=CD:CF,
即9:3=(9-3):CF,
∴CF=2.
故答案为:2.
点评 本题考查了相似三角形的判定与性质和等边三角形的性质.此题利用了“两角法”证得两个三角形相似.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
14.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{9}$ |
18.下列四个点中,位于第三象限的是( )
| A. | (2015,2014) | B. | (2014,-2015) | C. | (-2014,-2015) | D. | (-2015,2014) |
15.点P为直线l外一点,点A、B、C为直线上三点,PA=3cm,PB=4cm,PC=5cm,则点P到直线l的距离为( )
| A. | 2cm | B. | 3cm | C. | 小于3cm | D. | 不大于3cm |
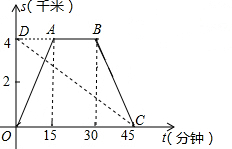 玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
玉环中学学生小林从学校出发到玉环图书馆查阅资料,同时他的同学小丽刚好从玉环图书馆查完资料沿同一条路回学校.学校与玉环图书馆的路程是4千米,小林骑自行车,小丽步行,当小林沿原路回到学校时,小丽也刚好回到学校,图中折线O-A-B-C和线段DC分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题: