题目内容
3.二次函数y=x2+mx+n的图象的顶点在直线y=-4上,该图象与直线y=x+2,y=-$\frac{1}{2}$x+1在0≤x≤2内各有一个交点,则m的取值范围是-8≤m≤-2$\sqrt{6}$或-4+4$\sqrt{2}$≤m$≤2\sqrt{5}$.分析 根据二次函数y=x2+mx+n的图象的顶点在直线y=-4上,确定n=$\frac{{m}^{2}-16}{4}$,代入解析式中,分两种情况:
①当抛物线L1的左半部分与两直线在0≤x≤2内各有一个交点时,满足:x=0时,y=$\frac{{m}^{2}-16}{4}$≥2,x=2时,y≤0,列不等式组求出解集;
②当抛物线L2的右半部分与两直线在0≤x≤2内各有一个交点,则满足:当x=2时,y≥4,当x=0时,y≤1,
列不等式组求出解集即可.
解答  解:∵二次函数y=x2+mx+n的图象的顶点在直线y=-4上,
解:∵二次函数y=x2+mx+n的图象的顶点在直线y=-4上,
∴$\frac{4n-{m}^{2}}{4}$=-4,
∴n=$\frac{{m}^{2}-16}{4}$,
∴y=x2+mx+$\frac{{m}^{2}-16}{4}$,
如图所示:分两种情况:
①当抛物线L1的左半部分与两直线在0≤x≤2内各有一个交点,
则满足x=0时,y=$\frac{{m}^{2}-16}{4}$≥2,
x=2时,y≤0,
即$\left\{\begin{array}{l}{\frac{{m}^{2}-16}{4}≥2}\\{4+2m+\frac{{m}^{2}-16}{4}≤0}\end{array}\right.$,
解得:-8≤m≤-2$\sqrt{6}$;
②当抛物线L2的右半部分与两直线在0≤x≤2内各有一个交点,
则满足:当x=2时,y≥4,
当x=0时,y≤1,
即$\left\{\begin{array}{l}{4+2m+\frac{{m}^{2}-16}{4}≥4}\\{\frac{{m}^{2}-16}{4}≤1}\end{array}\right.$,
解得:-4+4$\sqrt{2}$≤m$≤2\sqrt{5}$;
综上所述,则m的取值范围是:-8≤m≤-2$\sqrt{6}$或-4+4$\sqrt{2}$≤m$≤2\sqrt{5}$;
故答案为:-8≤m≤-2$\sqrt{6}$或-4+4$\sqrt{2}$≤m$≤2\sqrt{5}$.
点评 本题是二次函数和一次函数的综合题,考查了二次函数和一次函数的图象的性质,有难度,根据已知条件,利用数形结合的思想解决此题,并与不等式组相结合,利用不等式组的解集确定m的取值范围.

| A. | -3与-$\frac{1}{3}$ | B. | 3和|-3| | C. | -1与-|-1| | D. | -$\frac{1}{2}$和|-$\frac{1}{2}$| |
 如图:
如图: 如图,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,则△ADE的周长等于8.
如图,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,则△ADE的周长等于8.
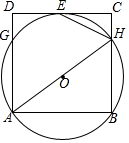 如图,过矩形ABCD顶点A,B的⊙O与CD相切于点E,与AD,BC分别相交于点G,H,连接EH,AH.
如图,过矩形ABCD顶点A,B的⊙O与CD相切于点E,与AD,BC分别相交于点G,H,连接EH,AH. 如图,已知△ABC中,AB=AC=8厘米,BC=6厘米,点D为AB 的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时,另一个点也随之停止运动.设运动时间为t.
如图,已知△ABC中,AB=AC=8厘米,BC=6厘米,点D为AB 的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时,另一个点也随之停止运动.设运动时间为t.