题目内容
6.已知|a+$\frac{1}{2}$|+(b-3)2=0,化简下面的式子并求值:[(2a+b)2-(b+2a)(2a-b)-6b]÷2b.
分析 直接利用绝对值以及偶次方的性质得出a,b的值,再利用整式乘法运算法则化简,再利用整式除法运算法则求出答案.
解答 解:∵|a+$\frac{1}{2}$|+(b-3)2=0,
∴a=-$\frac{1}{2}$,b=3,
[(2a+b)2-(b+2a)(2a-b)-6b]÷2b
=[4a2+4ab+b2-(4a2-b2)-6b]÷2b
=(2b2+4ab-6b)÷2b
=b+2a-3,
将a=-$\frac{1}{2}$,b=3,代入上式可得:
原式=3+2×(-$\frac{1}{2}$)+3
=5.
点评 此题主要考查了整式的混合运算,正确掌握整式乘法运算法则是解题关键.

练习册系列答案
相关题目
1.如图①,2条直线相交有1个交点,增加1条直线增加2个交点(图②),增加的交点数等于原直线条数2,所以三条直线最多有3个交点;
如图③,再增加1条直线,增加3个交点,增加的交点数等于原直线数3,所以4条直线最多有6个交点.
(1)根据这个规律,请继续把这个表格填完整.
(2)若有n条直线相交,最多有多少个交点?n=2013时,最多有多少个交点?

如图③,再增加1条直线,增加3个交点,增加的交点数等于原直线数3,所以4条直线最多有6个交点.
(1)根据这个规律,请继续把这个表格填完整.
| 直线条数 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 最多交点数 | 1 | 3 | 6 | 10 | 15 | 21 | … |

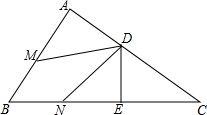 如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.
如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE. 已知:⊙O的半径是3,AB是⊙O的一条直径,CD是弦,且CD∥AB.若∠DAC=20°,则图中阴影部分的面积为π.
已知:⊙O的半径是3,AB是⊙O的一条直径,CD是弦,且CD∥AB.若∠DAC=20°,则图中阴影部分的面积为π. 如图是长方体的展开图,那么这个长方体的A面的对面是F面,B面的对面是D面,C面的对面是E面.
如图是长方体的展开图,那么这个长方体的A面的对面是F面,B面的对面是D面,C面的对面是E面.