题目内容
6. 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
分析 如图作EM⊥AD于M,交BC于N.在Rt△BEN中,求出BN,EN,利用勾股定理即可解决问题.
解答 解:如图作EM⊥AD于M,交BC于N.
∵△ADE是等边三角形,
∴AM=DM=$\frac{1}{2}$,BN=CN=$\frac{1}{2}$,EN=$\frac{\sqrt{3}}{2}$,
∴EN=1+$\frac{\sqrt{3}}{2}$,
在Rt△BNE中,BE=$\sqrt{B{N}^{2}+E{N}^{2}}$=$\sqrt{(\frac{1}{2})^{2}+(1+\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
故答案为$\frac{\sqrt{6}+\sqrt{2}}{2}$.
点评 本题考查等边三角形的性质、正方形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.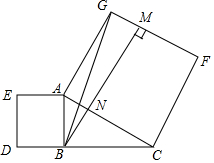 如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )
如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )
 如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )
如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )| A. | BG=CE | B. | BG⊥CE | ||
| C. | S正方形ABDE>S四边形ANMG | D. | BC2=CF•FM |
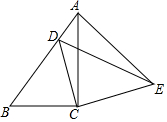 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$.
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕直角顶点C顺时针旋转得到△EDC,此时点B的对应点D恰好落在边AB上,连接AE,则AE的长为$\frac{12}{5}$. 如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4.
如图,正方形ABCD中,点M沿A-D-C运动到C,AN⊥BM,点P为AN的中点,AB=4,则点P的运动的路径长为4. 如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.
如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.