题目内容
11.已知关于x的多项式3x2-mx+n因式分解的结果为(3x+2)(x-1),则m、n的值分别为1,-2.分析 将(3x+2)(x-1)展开,则3x2-mx+n=3x2-x-2,从而求出m、n的值.
解答 解:∵(3x+2)(x-1)=3x2-x-2,
∴3x2-mx+n=3x2-x-2,
∴m=1,n=-2,
故答案为1,-2.
点评 本题考查了因式分解的应用,知道因式分解前后两式相等是解题的关键.

练习册系列答案
相关题目
1.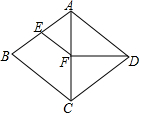 如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
 如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 15° |
 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.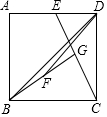 如图,在正方形ABCD中,E为AD的中点,G为CE的中点,F为BG的中点,连结DF,DB,若S△BGC=2,则边长BC=2$\sqrt{2}$,S△BFD=$\frac{1}{2}$.
如图,在正方形ABCD中,E为AD的中点,G为CE的中点,F为BG的中点,连结DF,DB,若S△BGC=2,则边长BC=2$\sqrt{2}$,S△BFD=$\frac{1}{2}$.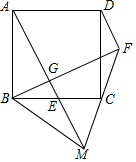 如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,则FD的长为2$\sqrt{5}$.
如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,则FD的长为2$\sqrt{5}$.