题目内容
16. 如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.
如图,已知:G是△ABC的重心,GE∥AC,则DE:BD=1:3.
分析 根据重心的概念得到AG=2GD,BD=DC,根据平行线分线段成比例定理列出比例式,计算即可.
解答 解:∵G是△ABC的重心,
∴AG=2GD,BD=DC,
∵GE∥AC,
∴$\frac{DE}{DC}$=$\frac{DG}{DA}$=$\frac{1}{3}$,
∴DE:BD=1:3,
故答案为:1:3.
点评 本题考查的是三角形的重心的概念和性质、平行线分线段成比例定理的应用,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
1.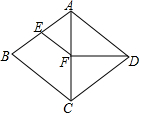 如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
 如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 15° |
5.下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则cos∠ABC的值是$\frac{\sqrt{195}}{25}$.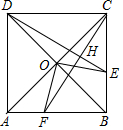 如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.
如图,正方形ABCD的对角线AC,BD相交于点O,点E在BC边上,连接DE,作CF⊥DE于点H,H交边AB于点F,连接OE,OF.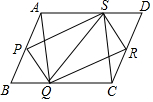 如图,平行四边形PQRS四个顶点恰好分别落在平行四边形ABCD的四条边上,请你判断以A、Q、C、S为顶点的四边形是什么形状,并说明理由.
如图,平行四边形PQRS四个顶点恰好分别落在平行四边形ABCD的四条边上,请你判断以A、Q、C、S为顶点的四边形是什么形状,并说明理由.