题目内容
20.点A及点B的坐标分别为(-2,6)及(3,8).A向下平移13单位至A′,B绕原点顺时针方向旋转90°至B′.(a)写出A′及B′的坐标
(b)证明AB平行于A′B′.
分析 (a)根据点A及点B的坐标分别为(-2,6)及(3,8),A向下平移13单位至A′,B绕原点顺时针方向旋转90°至B′,即可得到A′及B′的坐标;
(b)先根据待定系数法,分别求得直线AB的解析式为y=$\frac{2}{5}$x+$\frac{34}{5}$,直线A′B′的解析式为y=$\frac{2}{5}$x-$\frac{31}{5}$,根据系数k的值相等可得AB平行于A′B′.
解答 解:(a)∵点A及点B的坐标分别为(-2,6)及(3,8),
∴A向下平移13单位可得A′(-2,-7),B绕原点顺时针方向旋转90°可得B′(8,-3).
(b)设直线AB的解析式为y=kx+b,
把(-2,6),(3,8)代入,
可得$\left\{\begin{array}{l}{6=-2k+b}\\{8=3k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{5}}\\{b=\frac{34}{5}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{2}{5}$x+$\frac{34}{5}$;
设直线A′B′的解析式为y=mx+n,
把(-2,-7),(8,-3)代入,
可得$\left\{\begin{array}{l}{-7=-2m+n}\\{-3=8m+n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{2}{5}}\\{n=-\frac{31}{5}}\end{array}\right.$,
∴直线A′B′的解析式为y=$\frac{2}{5}$x-$\frac{31}{5}$,
∵两直线的系数k的值相等,
∴AB∥A′B′.
点评 本题主要考查了坐标与图形变化,两直线平行问题,解题时注意:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2.

 新思维寒假作业系列答案
新思维寒假作业系列答案| 第一次提现 | 第二次提现 | 第三次提现 | |
| 提现金额(元) | a | b | a+2b |
| 手续费(元) | 0 | 0.3 | 1.8 |
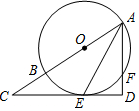 如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C. 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.