题目内容
14.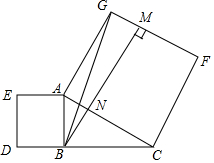 如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )
如图,在Rt△ABC中,∠ABC=90°,分别以AB、AC为边向外作正方形ABDE和正方形ACFG,过点B作BM⊥GF,垂足为M,BM交AC于点N,连接BG,CE,下列结论中,不正确的是( )| A. | BG=CE | B. | BG⊥CE | ||
| C. | S正方形ABDE>S四边形ANMG | D. | BC2=CF•FM |
分析 设CE,BG交于H,根据正方形的性质得到AB=AE,AG=AC,∠EAB=∠CAG=90°,得到∠EAC=∠BAG,根据全等三角形的性质得到BG=CE,故正确;推出A,E,B,H四点共圆,根据圆周角定理得到BG⊥CE,故正确;根据射影定理得到AB2=AN•AG,求得S正方形ABDE=S四边形ANMG,故错误;根据射影定理得到BC2=CN•AC,等量代换得到BC2=CF•FM,故正确.
解答 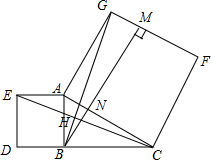 解:设CE,BG交于H,
解:设CE,BG交于H,
∵在正方形ABDE和正方形ACFG中,
AB=AE,AG=AC,∠EAB=∠CAG=90°,
∴∠EAC=∠BAG,
在△EAC与△BAG中,$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAG}\\{AC=AG}\end{array}\right.$,
∴BG=CE,故正确;
∠AEH=∠ABH,
∴A,E,B,H四点共圆,
∴∠BHE=90°,
∴BG⊥CE,故正确;
∵BM⊥GF,AC∥GF,
∴BN⊥AC,
∵∠ABC=90°,BN⊥AC,
∴AB2=AN•AG,
∴S正方形ABDE=S四边形ANMG,故错误;
∵∠ABC=90°,BN⊥AC,
∴BC2=CN•AC,
∵AC=CF,FM=CN,
∴BC2=CF•FM,故正确.
故选C.
点评 本题考查了全等三角形的判定与性质,射影定理,正方形的性质,正确的识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.越来越多的人用微信聊天、转账、付款等.把微信账户里的钱转到银行卡叫做提现.自2016年3月1日起,每个微信账户有1000元的免费提现额度,当累计提现超过这个额度时,超出的部分需要付0.1%的手续费.小明自2016年3月1日至今,用自己的一个微信账户共提现3次,3次的提现金额和手续费如下表:
用二元一次方程组的相关知识求表中a、b的值.
| 第一次提现 | 第二次提现 | 第三次提现 | |
| 提现金额(元) | a | b | a+2b |
| 手续费(元) | 0 | 0.3 | 1.8 |
 如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
如图,在正方形ABCD外侧作等边三角形ADE,AD=1,AC,BE相交于点F,则BE=$\frac{\sqrt{6}+\sqrt{2}}{2}$.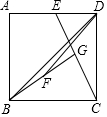 如图,在正方形ABCD中,E为AD的中点,G为CE的中点,F为BG的中点,连结DF,DB,若S△BGC=2,则边长BC=2$\sqrt{2}$,S△BFD=$\frac{1}{2}$.
如图,在正方形ABCD中,E为AD的中点,G为CE的中点,F为BG的中点,连结DF,DB,若S△BGC=2,则边长BC=2$\sqrt{2}$,S△BFD=$\frac{1}{2}$.