题目内容
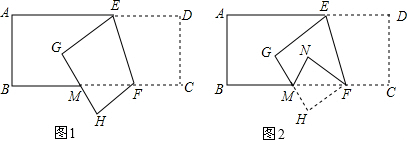
11．
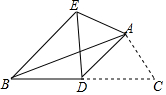如图，已知AD是△ABC的中线，∠ADC=45°，把△ADC沿AD所在直线对折，点C落在点E的位置，求∠EBC的度数．
分析 根据翻折不变性，可知△ADC≌△ADE，于是DE=DC，又因为AD是△ABC的中线，可知BD=CD，于是有BD=DE，进而求出∠EBC的度数．
解答 解：根据翻折不变性，可知△ADC≌△ADE，
∴DE=DC，∠ADE=∠ADC=45°，
∴∠EDC=90°，
又∵AD是△ABC的中线，
∴BD=CD，
于是，BD=DE，
∴∠EBC=45°．
点评 此题考查了翻折变换，找到变化过程中的不变量是解答此类问题的关键，同时要寻找图形中的直角三角形．
练习册系列答案
相关题目
16．
如图所示是某长方体形状包装盒的表面展开图，根据图中的数据，该包装盒的容积是（包装盒材料的厚度忽略不计）（ ）
如图所示是某长方体形状包装盒的表面展开图，根据图中的数据，该包装盒的容积是（包装盒材料的厚度忽略不计）（ ）| A． | 40×70×80 | B． | 80×80×40 | C． | 40×40×70 | D． | 70×70×80 |
20．
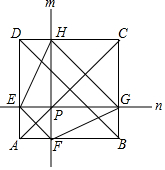如图，P为边长为4的正方形ABCD的对角线AC上动点（不与A、C重合），过P作直线m、n，分别与AD、AB平行，与正方形各边分别交于E、F、G、H，在以下判断中，不正确的是（ ）
如图，P为边长为4的正方形ABCD的对角线AC上动点（不与A、C重合），过P作直线m、n，分别与AD、AB平行，与正方形各边分别交于E、F、G、H，在以下判断中，不正确的是（ ）| A． | P点变化时，四边形EFGH面积保持不变 | |
| B． | P点变化时，六边形DEFBGH面积有最大值12$\sqrt{2}$ | |
| C． | 点P位于正方形ABCD的中心时，DE=2 | |
| D． | P点变化时，六边形DEFBGH周长保持不变 |
