题目内容
 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax2+bx+4过A,B,C三点且AB=6.(1)求⊙P的半径R的长;
(2)若点E在y轴上,且△ACE是等腰三角形,试写出所有点E的坐标.
考点:圆的综合题
专题:
分析:(1)在函数y=ax2+bx+4中令x=0,解得y=4,则OC=PD=4,连接PA,在直角三角形△PAD中,根据勾股定理就可以得到PA的长.即圆的半径;
(2)根据等腰三角形的性质,把AC分别看作底和腰进行讨论.
(2)根据等腰三角形的性质,把AC分别看作底和腰进行讨论.
解答:解:(1)如图,连接AP,

∵四边形ODPC为矩形,
∴PD⊥AB,
∴AD=BD=
AB=3,
又∵抛物线y=ax2+bx+4经过A,B,C三点,
∴C(0,4),
即OC=4,
∴PD=OC=4,
∴由勾股定理得AP=5,
∴⊙P的半径R的长为5;
(2)由(1)得OA=PC-AD=5-3=2,OC=4,则AC=
=2
,
设E点坐标为(0,y),当△ACE是等腰三角形时,有三种情况,
①当AC=CE时,则有|y-4|=2
,解得y=4+2
和y=4-2
,此时E点坐标为E1(0,4+2
),E2(0,4-2
);
②当AC=AE时,因为O为AE中点,所以OE=OC=4,此时E点坐标为E3(0,-4);
③当CE=AE时,则CE=|y-4|,OE=|y|,OA=2,在Rt△OAE中由勾股定理可得:|y-4|2=|y|2+22,解得y=
,此时E点坐标为(0,
);
综上可知E点的坐标为E1(0,4+2
),E2(0,4-2
),E3(0,-4)(0,
).

∵四边形ODPC为矩形,
∴PD⊥AB,
∴AD=BD=
| 1 |
| 2 |
又∵抛物线y=ax2+bx+4经过A,B,C三点,
∴C(0,4),
即OC=4,
∴PD=OC=4,
∴由勾股定理得AP=5,
∴⊙P的半径R的长为5;
(2)由(1)得OA=PC-AD=5-3=2,OC=4,则AC=
| OA2+OC2 |
| 5 |
设E点坐标为(0,y),当△ACE是等腰三角形时,有三种情况,
①当AC=CE时,则有|y-4|=2
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
②当AC=AE时,因为O为AE中点,所以OE=OC=4,此时E点坐标为E3(0,-4);
③当CE=AE时,则CE=|y-4|,OE=|y|,OA=2,在Rt△OAE中由勾股定理可得:|y-4|2=|y|2+22,解得y=
| 3 |
| 2 |
| 3 |
| 2 |
综上可知E点的坐标为E1(0,4+2
| 5 |
| 5 |
| 3 |
| 2 |
点评:本题主要考查垂径定理及矩形的性质、等腰三角形的性质的综合应用,熟练掌握垂径定理即垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧是解题的关键.

练习册系列答案
相关题目
若3x3-kx2+4被3x-1除后余3,则k的值为( )
| A、2 | B、4 | C、9 | D、10 |
下列说法正确的是( )
| A、0.720精确到千位 |
| B、3.6万精确到个位 |
| C、5.078精确到千分位 |
| D、3.3998精确到百分位为3.39 |
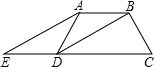 如图,在等腰梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.若∠E=30°,EC=12,求梯形ABCD的面积.
如图,在等腰梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.若∠E=30°,EC=12,求梯形ABCD的面积.