题目内容
7.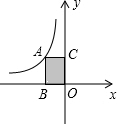 如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )
如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )| A. | -3 | B. | 3 | C. | 9 | D. | -9 |
分析 根据反比例函数k的几何意义得到|k|=3,然后根据反比例函数的性质确定k的值.
解答 解:根据题意得|k|=3,
而k<0,
所以k=-3.
故选A.
点评 本题考查了反比例函数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.依次连接菱形的各边中点,得到的四边形是( )
| A. | 矩形 | B. | 平行四边形 | C. | 菱形 | D. | 梯形 |
12. 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )| A. | $\sqrt{2}-3$ | B. | 2$\sqrt{2}$-1 | C. | 3$\sqrt{2}$-3 | D. | 2-$\sqrt{2}$ |
7.若ab<0,bc=0,则直线ax+by+c=0,通过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二、三象限 | D. | 第一、二、四象限 |

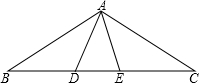 如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.
如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.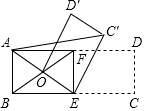 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.