题目内容
15.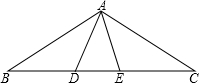 如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.
如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,求∠C的度数.
分析 根据SAS即可推出△ABD≌△ACE,推出AB=AC,∠B=∠C,求出BE=DC,根据SSS推出△ABE≌△ACD,推出∠BAE=∠CAD=70°,根据三角形外角性质即可求出∠C.
解答 解:在△ABD和△ACE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BDA=∠AEC}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AB=AC,∠B=∠C,
∵BD=CE,
∴BD+DE=EC+DE,
∴BE=DC,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AE=AD}\\{AB=AC}\\{BE=CD}\end{array}\right.$
∴△ABE≌△ACD,
∴∠BAE=∠CAD=70°,
∵∠ADB=100°,
∴∠C=∠ADB-∠CAD=100°-70°=30°.
点评 此题考查等腰三角形的判定和性质,全等三角形的性质和判定,三角形外角性质,三角形内角和定理的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
5.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )


| A. | 2016 个 | B. | 2015 个 | C. | 2014 个 | D. | 2013个 |
6.下列各组单项式:①9a2b3与a3b2;②-3x2yz与-3x2y;③(-a)5与(-8)5;④-13x2y与0.7yx2;⑤2016与-$\frac{3}{5}$中,是同类项的是( )
| A. | ①⑤ | B. | ①②④ | C. | ④⑤ | D. | ③④⑤ |
16.下列变形中正确的是( )
| A. | 由3x=4x+1得4x-3x=1 | B. | 由2(3-x)=5得6-x=5 | ||
| C. | 由-4x<3得$x>-\frac{3}{4}$ | D. | 由3x>-2得$x<-\frac{2}{3}$ |
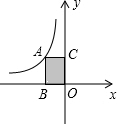 如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )
如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )