题目内容
12. 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )| A. | 130° | B. | 125° | C. | 120° | D. | 115° |
分析 在优弧$\widehat{AB}$上取一点D,连接AD、BD,根据圆周角定理求出∠D的度数,根据圆内接四边形的性质计算即可.
解答 解: 在优弧$\widehat{AB}$上取一点D,连接AD、BD,
在优弧$\widehat{AB}$上取一点D,连接AD、BD,
∠D=$\frac{1}{2}$∠AOB=65°,
∵四边形ADBC是⊙O的内接四边形,
∴∠D+∠ACB=180°,
∴∠ACB=115°,
故选:D.
点评 本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.我们学习了整式的乘法后,可进行如下计算:(a+b)1=a+b;(a+b)2=a2+2ab+b2;(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3;
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
上表称为“杨辉三角”,揭示了二项式乘方展开式的规律.
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
…
如果我们对(a+b)n (n取正整数)的计算结果中各项系数进一步研究,可以列出下表:
| (a+b)1=a+b | 1 | 1 | ||||||||
| (a+b)2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| (a+b)3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| … | … |
(1)请仔细观察表中的规律,写出(a+b)4展开式中所缺的系数:(a+b)4=a4+a3b+a2b2+ab3+b4
(2)请写出(a+b)5的展开式:(a+b)5=(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)当n=1、2、3、4、…时,(a+b)n展开式的第三项系数分别为0、1、3、6、…,猜想(a+b)n展开式的第三项系数为$\frac{n(n-1)}{2}$(用含n的代数式表示);
(4)当n=1、2、3、4、…时,(a+b)n展开式的各项系数之和分别为2、4、8、16、…,猜想(a+b)n展开式的各项系数之和为2n(用含n的代数式表示).
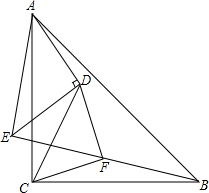 如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.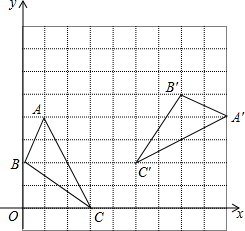 如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0).
如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0). 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD. 如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,求S四边形DBCE的值.
如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,求S四边形DBCE的值.