题目内容
4. 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=AD=8,求CD的长.
分析 (1)首先证明△ABD≌△ACD,得到∠BAD=∠CAD,再根据等腰三角形的性质即可证明;
(2)四边形BFCD的形状是菱形,首先证明△BFE≌△CDE,得到BF=DC,可知四边形BFCD是平行四边形,易证BD=CD,可证明结论;
(3)设DE=x,则根据CE2=DE•AE列方程求出DE,再用勾股定理求出CD即可.
解答 (1)证明:∵AD是直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)四边形BFCD是菱形.理由如下:
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中,
$\left\{\begin{array}{l}{∠FCE=∠DBE}\\{BE=BE}\\{∠BED=∠CEF=90°}\end{array}\right.$,
∴△BED≌△CEF,
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DE•AE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10-x),
解得:x=4,
在Rt△CED中,
CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=4$\sqrt{2}$.
点评 本题主要考查了圆的有关性质:垂径定理、圆周角定理,三角形全等的判定与性质,菱形的判定与性质,勾股定理,三角形相似的判定与性质,熟悉圆的有关性质是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.甲厂和乙厂都有某种仪器可供其他厂使用,其中甲厂可提供10台,乙厂可提供4台,已知丙厂需要8台,丁厂需要6台,从甲厂到丙厂、丁厂每台仪器需运费分别为400元和800元,乙厂到丙厂、丁厂每台仪器的运费分别为300元和500元.设甲厂运往丙厂的仪器为x台.
(1)请用含x的代数式填写下表中的空格:
(2)现计划用7600元运送这批仪器,请你设计一种调运方案,使丙厂、丁厂能得到所需的仪器,而且费用正好用完;
(3)试问有无可能使总运费为8000元?若可能,请求出甲厂运往丙厂的仪器台数;若不可能,请说明理由.
(1)请用含x的代数式填写下表中的空格:
| 起点/终点 | 丙厂 | 丁厂 |
| 甲厂 | x | 10-x |
| 乙厂 | 8-x | x-4 |
(3)试问有无可能使总运费为8000元?若可能,请求出甲厂运往丙厂的仪器台数;若不可能,请说明理由.
12. 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )| A. | 130° | B. | 125° | C. | 120° | D. | 115° |
16.如图的各组图形中,相似的是( )


| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (1)(3)(4) | D. | (1)(2)(4) |
 如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°.
如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°. 长汀的动车时代来了!据报道,2015年11月26日,赣(州)瑞(金)龙(岩)铁路进入试运行阶段.赣州到龙岩,乘快速列车的行程约为290km,动车开通后,动车的行程约为250km,运行时间比快速列车所用的时间减少了2.375h.若动车的平均速度是快速列车平均速度的2.5倍,求动车的平均速度.
长汀的动车时代来了!据报道,2015年11月26日,赣(州)瑞(金)龙(岩)铁路进入试运行阶段.赣州到龙岩,乘快速列车的行程约为290km,动车开通后,动车的行程约为250km,运行时间比快速列车所用的时间减少了2.375h.若动车的平均速度是快速列车平均速度的2.5倍,求动车的平均速度.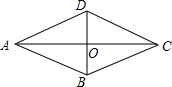 一个菱形的一条对角线长60cm.周长是200cm.求:
一个菱形的一条对角线长60cm.周长是200cm.求: