题目内容
用60m的篱笆围成一个一边靠墙、中间用篱笆隔开的矩形养鸡场.
(1)如果中间只有一道篱笆,如图1,并设矩形一边的长为xm,那么当x为何值时,养鸡场的面积最大?
(2)如果养鸡场中间有6道篱笆,如图2,并设矩形一边的长为xm,那么当x为何值时,养鸡场的面积最大?

(1)如果中间只有一道篱笆,如图1,并设矩形一边的长为xm,那么当x为何值时,养鸡场的面积最大?
(2)如果养鸡场中间有6道篱笆,如图2,并设矩形一边的长为xm,那么当x为何值时,养鸡场的面积最大?

考点:二次函数的应用
专题:
分析:(1)当养鸡场的中间有一道篱笆时,利用鸡场的长x表示出鸡场的宽,列出鸡场面积y关于x的二次函数式,利用函数知识即可解决问题;
(2)类似于(1),当养鸡场的中间有6道篱笆时,利用鸡场的长x表示出鸡场的宽,列出鸡场面积y关于x的二次函数式,利用函数知识即可解决问题.
(2)类似于(1),当养鸡场的中间有6道篱笆时,利用鸡场的长x表示出鸡场的宽,列出鸡场面积y关于x的二次函数式,利用函数知识即可解决问题.
解答:解:(1)设养鸡场的面积为y.
∵当养鸡场的长为x米时,宽为
米,
∴面积y=x•
=--
(x-30)2+300
∴当x=30时,y取得最大值300,
即当x=30时,养鸡场的面积最大.
(2)∵当养鸡场的长为x米时,宽为
米,
∴面积y=x•
=-
(x-30)2+
∴当x=30时,y取得最大值
,
即当x=30时,养鸡场的面积最大.
∵当养鸡场的长为x米时,宽为
| 60-x |
| 3 |
∴面积y=x•
| 60-x |
| 3 |
=--
| 1 |
| 3 |
∴当x=30时,y取得最大值300,
即当x=30时,养鸡场的面积最大.
(2)∵当养鸡场的长为x米时,宽为
| 60-x |
| 8 |
∴面积y=x•
| 60-x |
| 8 |
=-
| 1 |
| 8 |
| 900 |
| 8 |
∴当x=30时,y取得最大值
| 900 |
| 8 |
即当x=30时,养鸡场的面积最大.
点评:考查了二次函数在现实生活中的实际应用问题;解题的关键是将实际问题转化为数学问题以后,准确列出二次函数关系式,正确运用二次函数的有关性质来解题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为( )
| A、1 | ||
| B、-1 | ||
| C、1或-1 | ||
D、
|
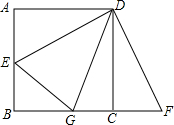 如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论.
如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论. 如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证:
如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证: 如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则DP=
如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则DP=