题目内容
甲乙两船从同一港口A出发,甲船以10海里/时的速度向东航行2小时后到达港口M,乙船比甲船晚出发30分钟,以相同的速度向南航行,在甲到达港口M同时,乙到达港口N,则M、N两港口相距多少海里?
考点:勾股定理的应用
专题:
分析:根据题意得出AM,AN的长,再利用勾股定理求出MN即可.
解答: 解:如图所示:∵甲船以10海里/时的速度向东航行2小时后到达港口M,乙船比甲船晚出发30分钟,以相同的速度向南航行,在甲到达港口M同时,乙到达港口N,
解:如图所示:∵甲船以10海里/时的速度向东航行2小时后到达港口M,乙船比甲船晚出发30分钟,以相同的速度向南航行,在甲到达港口M同时,乙到达港口N,
∴AM=2×10=20(海里),AN=15海里,∠A=90°,
∴在Rt△AMN中,MN=
=25(海里),
答:M、N两港口相距25海里.
 解:如图所示:∵甲船以10海里/时的速度向东航行2小时后到达港口M,乙船比甲船晚出发30分钟,以相同的速度向南航行,在甲到达港口M同时,乙到达港口N,
解:如图所示:∵甲船以10海里/时的速度向东航行2小时后到达港口M,乙船比甲船晚出发30分钟,以相同的速度向南航行,在甲到达港口M同时,乙到达港口N,∴AM=2×10=20(海里),AN=15海里,∠A=90°,
∴在Rt△AMN中,MN=
| AN2+AM2 |
答:M、N两港口相距25海里.
点评:此题主要考查了勾股定理的应用,得出AN,AM的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

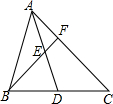 如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=
如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF= 如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且
如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且
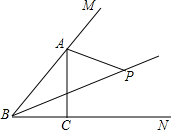 如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.