题目内容
 如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证:
如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,DE⊥BD,点D在AB边上,连结EC,取EC中点F,求证:(1)AF=DF;
(2)AF⊥DF.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)连接BF,延长DF交AC于点G,利用等腰三角形的性质得到∠DEF=∠DBF,可证得DG∥BC,得出△ADG为等腰在角形,再证明△DEF≌△GFC,得到DF=FG,可得到结论;
(2)由(1)结合F为DG中点,可得到AF=DF=FG.
(2)由(1)结合F为DG中点,可得到AF=DF=FG.
解答: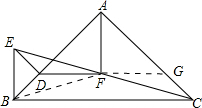 证明:(1)连接BF,延长DF交AC于点G,
证明:(1)连接BF,延长DF交AC于点G,
∵∠EBD=∠ABC=45°,
∴∠EBC=90°,
在RT△EBC中,F为斜边中点,
∴BF=EF,
∴∠FBC=∠FCB,
∴∠DFE=∠DFB,
∵∠EFB=∠FBC+∠FCB,
∴∠DFE+∠DFB=∠FBC+∠FCB,
∴2∠DFB=2∠FBC,
则∠DFB=∠FBC,
∴DG∥BC,
∵△BAC为等腰直角三角形,且DG∥BC,AB=AC,
∴AD=AG,BD=CG,
∵BD=DE,
∴DE=CG,
∵∠BDE=∠CAB=90°,
∴DE∥AC,
∴∠DEF=∠GCF,
在△DEF和△GCF中,
∴△DEF≌△GCF(SAS),
∴DF=FG,
∵△DAG为等腰直角三角形,
∴AF⊥DG;
(2)∵F为DG中点,
∴在RT△DAG中,AF=DF.
 证明:(1)连接BF,延长DF交AC于点G,
证明:(1)连接BF,延长DF交AC于点G,∵∠EBD=∠ABC=45°,
∴∠EBC=90°,
在RT△EBC中,F为斜边中点,
∴BF=EF,
∴∠FBC=∠FCB,
∴∠DFE=∠DFB,
∵∠EFB=∠FBC+∠FCB,
∴∠DFE+∠DFB=∠FBC+∠FCB,
∴2∠DFB=2∠FBC,
则∠DFB=∠FBC,
∴DG∥BC,
∵△BAC为等腰直角三角形,且DG∥BC,AB=AC,
∴AD=AG,BD=CG,
∵BD=DE,
∴DE=CG,
∵∠BDE=∠CAB=90°,
∴DE∥AC,
∴∠DEF=∠GCF,
在△DEF和△GCF中,
|
∴△DEF≌△GCF(SAS),
∴DF=FG,
∵△DAG为等腰直角三角形,
∴AF⊥DG;
(2)∵F为DG中点,
∴在RT△DAG中,AF=DF.
点评:本题主要考查三角形全等的判定和性质,证得△ADG为等腰三角形是解题的关键.

练习册系列答案
相关题目
多项式(x+y-z)(x-y+z)-(y+z-x)(z-x-y)的公因式是( )
| A、x+y-z | B、x-y+z |
| C、y+z-x | D、不存在 |
 如图,D、E、F分别是等边△ABC各边上的点,且AD=BE=CF,当点D位于何处时,△EFD的面积最小?
如图,D、E、F分别是等边△ABC各边上的点,且AD=BE=CF,当点D位于何处时,△EFD的面积最小?
 如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且
如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且