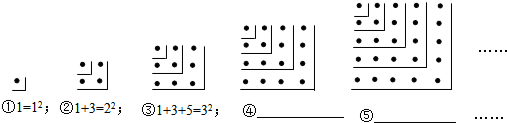
题目内容
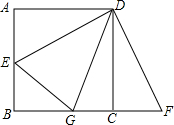 如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论.
如图,已知正方形ABCD的边长为8,E为AB上一点,点B、C、F在同一条直线上,且AE=CF,当∠EDG为多少度时,存在AE+CG=EG,并证明这个结论.考点:全等三角形的判定与性质,正方形的性质
专题:
分析:根据正方形性质得出AD=DC,∠A=∠ADC=∠BCD=∠DCF=90°,证△DAE≌△DCF,推出DE=DF,∠ADE=∠CDF,求出∠GDF=∠EDG,证△EDG≌△FDG,推出EG=GF即可.
解答:答:当∠EDG为45°时,存在AE+CG=EG,
证明:∵四边形ABCD是正方形,
∴AD=DC,∠A=∠ADC=∠BCD=∠DCF=90°,
在△DAE和△DCF中
∴△DAE≌△DCF,
∴DE=DF,∠ADE=∠CDF,
∵∠ADC=90°,∠EDG=45°,
∴∠ADE+∠CDG=45°,
∴∠GDF=∠CDG+∠CDF=45°=∠EDG,
在△EDG和△FDG中,
,
∴△EDG≌△FDG(SAS),
∴EG=GF,
∵GF=CG+CF=CG+AE,
∴AE+CG=EG,
即当∠EDG为45°时,存在AE+CG=EG.
证明:∵四边形ABCD是正方形,
∴AD=DC,∠A=∠ADC=∠BCD=∠DCF=90°,
在△DAE和△DCF中
|
∴△DAE≌△DCF,

∴DE=DF,∠ADE=∠CDF,
∵∠ADC=90°,∠EDG=45°,
∴∠ADE+∠CDG=45°,
∴∠GDF=∠CDG+∠CDF=45°=∠EDG,
在△EDG和△FDG中,
|
∴△EDG≌△FDG(SAS),
∴EG=GF,
∵GF=CG+CF=CG+AE,
∴AE+CG=EG,
即当∠EDG为45°时,存在AE+CG=EG.
点评:本题考查了正方形的性质,全等三角形的性质和判定的应用,题目比较典型,是一道比较好的题目.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
多项式(x+y-z)(x-y+z)-(y+z-x)(z-x-y)的公因式是( )
| A、x+y-z | B、x-y+z |
| C、y+z-x | D、不存在 |
 已知△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE的一边DE交直线a于点E,∠ADE=60°,若D在BC上,求证:CD+CE=CA.
已知△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE的一边DE交直线a于点E,∠ADE=60°,若D在BC上,求证:CD+CE=CA.
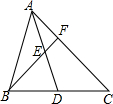 如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=
如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=