题目内容
已知方程组
的解x与y的和为正数,求a的范围.
|
考点:二元一次方程组的解,解一元一次不等式
专题:
分析:先将两个方程相加,得2x+2y=1-3a,即x+y=
(1-3a),再根据x与y的和为正数列出不等式
(1-3a)>0,解不等式即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:
,
将两个方程相加,得2x+2y=1-3a,即x+y=
(1-3a),
∵方程组
的解x与y的和为正数,
∴
(1-3a)>0,
解得a<
.
|
将两个方程相加,得2x+2y=1-3a,即x+y=
| 1 |
| 2 |
∵方程组
|
∴
| 1 |
| 2 |
解得a<
| 1 |
| 3 |
点评:本题考查了二元一次方程组的解的意义及一元一次不等式的解法,不解方程组,而利用方程组本身的特点,将两个方程直接相加,得出2x+2y=1-3a,即x+y=
(1-3a)能使计算简便.
| 1 |
| 2 |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
多项式(x+y-z)(x-y+z)-(y+z-x)(z-x-y)的公因式是( )
| A、x+y-z | B、x-y+z |
| C、y+z-x | D、不存在 |

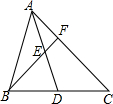 如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF=
如图,AD是△ABC中BC边上的中线,E为AD的中点,延长BE交AC于点F,AF= 如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且
如图,已知AB、CE是⊙O的直径,D是AC上一点,∠COD=60°,且