题目内容
11.已知,在△ABC中,CA=CB=10cm,O为AB的中点,E、F分别在直线AC、BC上,且∠EOF=2∠A.(1)若∠A=45°.
①如图(1),连接OC,当E、F分别在线段AC、BC上时,求证:△COE≌△BOF;
②如图(2),当E、F分别在AC延长线上和CB延长线上时,求CF-CE的值;
(2)如图(3),若∠A=30°,且E、F分别在AC延长线上和线段BC上,试说明CF与CE满足怎样的关系式.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)

分析 (1)要证明△COE≌△BOF只要证明:CO=BO,∠EOC=∠FOB,∠ECO=∠B=45°即可.
(2)因为CF=CB+BF,所以要求CF-CE,只要证明CE=BF就可以了;
(3)利用四点共圆得到:△OEF是等边三角形,接下来只要证明CF-CE=CA,再利用直角三角形30度角的性质解决.
解答 (1)证明: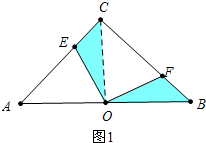 连接CO.
连接CO.
∵CA=CB,∠A=45°
∴∠A=∠B=45°,∠ACB=90°,
∵AO=OB,
∴OC=OA=OB,∠ACO=∠BCO=45°,CO⊥AB,
∵∠EOF=2∠A=90°,∠COB=90°,
∴∠EOF=∠COB,
∴∠EOC=∠BOF,
在△EOC和△FOB中,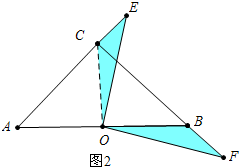
$\left\{\begin{array}{l}{∠ECO=∠B}\\{CO=OB}\\{∠EOC=∠FOB}\end{array}\right.$,
∴△EOC≌△FOB.
(2)如图2中,连接CO,∵∠ACO=∠ABC=45°,
∴∠ECO=∠OBF=135°,
∵∠COB=∠EOF=90°,
∴∠COE=∠BOF,
在△EOC和△FOB中
$\left\{\begin{array}{l}{∠ECO=∠B}\\{CO=OB}\\{∠EOC=∠FOB}\end{array}\right.$,
∴△EOC≌△FOB.
∴EC=BF,
∴CF-EC=BC+BF-EC=BC=10cm.
(3)在CF上截取CM=CO,连接OM.
∵CA=CB,∠A=30°,
∴∠A=∠B=30°,∠ACB=120°,
∵AO=OB,
∴∠ACO=∠BCO=60°
∴∠ECB=180°-∠ACB=60°,
∵∠EOF=2∠A=60°,
∴∠ECF=∠EOF,
∴E、C、O、F四点共圆,
∴∠OEF=∠OCB=60°,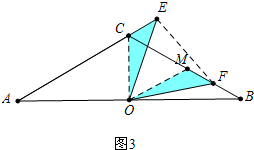
∴△OEF是等边三角形,
∴OE=OF,
∵OC=CM,∠OCM=60°,
∴△COM是等边三角形,
∴∠COM=60°=∠EOF,OC=OM=CM,
∴∠COE=∠MOF,
在△COE和△MOF中,
$\left\{\begin{array}{l}{CO=OM}\\{∠COE=∠MOF}\\{OE=OF}\end{array}\right.$,
∴△COE≌△MOF,
∴CE=MF,
∴CF-CE=CM+MF-CE=CM=CO,
在RT△ACO中.∵AC=10,∠A=30°,
∴CO=$\frac{1}{2}$AC=5,
∴CF-CE=5.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、以及四点共圆等知识,第三个问题中,利用四点共圆是解决问题的关键.

| A. | 0到1之间 | B. | 1到2之间 | C. | 2到3之间 | D. | 3至4之间 |
 如图,△AOB中,∠AOB=120°,BD,AC是两条高,连接CD,若AB=4,则DC的长为( )
如图,△AOB中,∠AOB=120°,BD,AC是两条高,连接CD,若AB=4,则DC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{4}$ |
| A. | 开口方向向下 | B. | 形状与y=x2相同 | C. | 顶点(-1,4) | D. | 对称轴是x=1 |
 如图,用长为12m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
如图,用长为12m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.