题目内容
11．用公式法求函数y=3x2-3x-$\frac{5}{4}$的最小值．分析 直接代入顶点坐标公式计算即可解答．
解答 解：∵a=3，b=-3，c=-$\frac{5}{4}$，
∴$\frac{4ac-{b}^{2}}{4a}$
=$\frac{4×3×（-\frac{5}{4}）-（-3）^{3}}{4×3}$
=-2．
∴函数y=3x2-3x-$\frac{5}{4}$的最小值为-2．
点评 此题考查二次函数的性质，掌握顶点坐标公式是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
2．
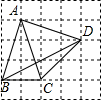如图，四边形ABCD的顶点都在正方形网格的格点上，则tan∠CBD的值为（ ）
如图，四边形ABCD的顶点都在正方形网格的格点上，则tan∠CBD的值为（ ）| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | $\frac{2\sqrt{5}}{5}$ |
19．下列说法正确的是（ ）
| A． | 8的立方根是±2 | B． | -1不存在立方根 | ||
| C． | 2的算术平方根是$±\sqrt{2}$ | D． | -25不存在平方根 |
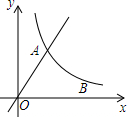如图，直线y=$\frac{3}{4}$x与双曲线y=$\frac{k}{x}$（x＞0）交于点A，将直线y=$\frac{3}{4}$x向右平移6个单位后，与双曲线y=$\frac{k}{x}$（x＞0）交于点B，与x轴交于点C，若A点到x轴的距离是B点到x轴的距离的2倍，那么k的值为（ ）
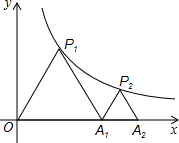如图，P1、P2是反比例函数y=$\frac{k}{x}$（k＞0）在第一象限图象上的两个点，点A1坐标为（4，0），若△P1OA1与△P2A1A2均为等边三角形，则点A2的横坐标为4$\sqrt{2}$．
如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中，从三个方向看不能得到的图形是（ ）
