题目内容
1．
如图，用长为12m的篱笆（虚线部分），两面靠墙围成矩形的苗圃．（1）设矩形的一边长为x（m），面积为y（m2），求y关于x的函数关系式，并写出自变量x的取值范围；
（2）当x为何值时，所围苗圃的面积最大，最大面积是多少？
分析 （1）根据矩形的面积=长乘以宽，篱笆只有两边，且其和为12，设一边为x，则另一边为（12-x），根据公式即可表示面积；
（2）根据函数性质求最值，可用公式法或配方法．
解答 解：（1）由已知，矩形的另一边长为（12-x）m
则y=x（12-x）=-x2+12x
自变量x的取值范围是0＜x＜12．
（2）∵y=-x2+12x=-（x-6）2+36
∴当x=6时（0＜x＜12），苗圃的面积最大，最大面积是36m2．
点评 本题主要考查二次函数的实际应用能力，运用函数性质求最值解决实际问题时常需考虑自变量的取值范围；二次函数求最值常用配方法和公式法．
练习册系列答案
相关题目
如图，已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A（1，8）、B（-4，m）．
9．
生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二，产生新的微生物（依次被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么标号为1535的微生物会出现在（ ）
生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二，产生新的微生物（依次被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么标号为1535的微生物会出现在（ ）| A． | 第7天 | B． | 第8天 | C． | 第9天 | D． | 第10天 |
16．在直角坐标系中，点A（2，1）向下平移2个单位长度后的坐标为（ ）
| A． | （4，1） | B． | （0，1） | C． | （2，3） | D． | （2，-1） |
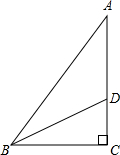如图，在Rt△ABC中，∠C=90°，BD是三角形的角平分线，交AC于点D，AD=2.2cm，AC=3.7cm，则点D到AB边的距离是1.5cm．
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AC=13，BC=5，BE⊥DC交DC的延长线于点E．