题目内容
3.已知在△ABC中,∠ACB=90°,AC=BC,以AC为一边,在同一平面内作等边△ACD,连接BD,则∠ADB的度数为45或135度.分析 根据等边三角形的性质得出DC=BC,进而得出∠CDB=15°解答即可.
解答 解:如图: ∵等边△ACD,
∵等边△ACD,
∴DC=AC=AD,∠DCA=∠ADC=60°,
∵AC=BC,
∴DC=BC,
∴∠CDB=$\frac{1}{2}×(180°-60°-90°)$=15°,
∴∠ADB=60°-15°=45°,
在△ABC的里侧做等边三角形ACD,则角ADB=135°,
故答案为:45或135.
点评 此题考查等边三角形的性质,关键是根据等边三角形三边相等和三角相等解答.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.某工厂去年的利润为200万元.今年的总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.(说明:利润=总收入-总支出)
(1)若设去年的总收入为x万元,总支出为y万元,请完成下列表格(要求填化简结果):
(2)在(1)的基础上,求今年的总收入和总支出各是多少万元?
(1)若设去年的总收入为x万元,总支出为y万元,请完成下列表格(要求填化简结果):
| 总收入(单位:万元) | 总支出(单位:万元) | 利润(单位:万元) | |
| 去年 | x | y | 200 |
| 今年 | 1.2x | 0.9y | 780 |
8. 如图,第一象限的点P的坐标是(a,b),则tan∠POx等于( )
如图,第一象限的点P的坐标是(a,b),则tan∠POx等于( )
 如图,第一象限的点P的坐标是(a,b),则tan∠POx等于( )
如图,第一象限的点P的坐标是(a,b),则tan∠POx等于( )| A. | $\frac{a}{b}$ | B. | $\frac{b}{a}$ | C. | $\frac{a}{{\sqrt{{a^2}+{b^2}}}}$ | D. | $\frac{b}{{\sqrt{{a^2}+{b^2}}}}$ |
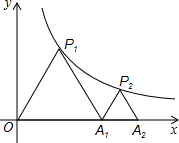 如图,P1、P2是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上的两个点,点A1坐标为(4,0),若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为4$\sqrt{2}$.
如图,P1、P2是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上的两个点,点A1坐标为(4,0),若△P1OA1与△P2A1A2均为等边三角形,则点A2的横坐标为4$\sqrt{2}$.
 如图,在四边形ABCD中,对角线AC,BD交于点E,AE=2,CE=3,AB=2,D到AC的距离为1,求四边形ABCD的面积.
如图,在四边形ABCD中,对角线AC,BD交于点E,AE=2,CE=3,AB=2,D到AC的距离为1,求四边形ABCD的面积. 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m). 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.