题目内容
9．已知a，b，c为△ABC的三边之长，且满足a4-b4-a2c2+b2c2=0，试判断△ABC的形状．分析 通过恒等变形把已知条件变为：（a2-b2）（a2+b2-c2）=0即可判断．
解答 解：∵a4-b4-a2c2+b2c2=0，
∴（a2+b2）（a2-b2）-c2（a2-b2）=0，
∴（a2-b2）（a2+b2-c2）=0，
∴a2-b2=0或a2+b2=c2．
∴a=b，或a2+b2=c2．
∴△ABC是等腰三角形或直角三角形．
点评 本题考查三角形的分类、因式分解等知识，利用分组分解是解题的关键．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
19．下列说法正确的是（ ）
| A． | 8的立方根是±2 | B． | -1不存在立方根 | ||
| C． | 2的算术平方根是$±\sqrt{2}$ | D． | -25不存在平方根 |
如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中，从三个方向看不能得到的图形是（ ）
4．某工厂去年的利润为200万元．今年的总收入比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元．（说明：利润=总收入-总支出）
（1）若设去年的总收入为x万元，总支出为y万元，请完成下列表格（要求填化简结果）：
（2）在（1）的基础上，求今年的总收入和总支出各是多少万元？
（1）若设去年的总收入为x万元，总支出为y万元，请完成下列表格（要求填化简结果）：
| 总收入（单位：万元） | 总支出（单位：万元） | 利润（单位：万元） | |
| 去年 | x | y | 200 |
| 今年 | 1.2x | 0.9y | 780 |
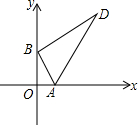Rt△ABD的两顶点A、B分别在x轴和y轴上运动，其中∠ABD=90°，∠D=30°，AB=4，则顶点D到原点O的距离的最大值和最小值的乘积为48．
8．
如图，第一象限的点P的坐标是（a，b），则tan∠POx等于（ ）
如图，第一象限的点P的坐标是（a，b），则tan∠POx等于（ ）| A． | $\frac{a}{b}$ | B． | $\frac{b}{a}$ | C． | $\frac{a}{{\sqrt{{a^2}+{b^2}}}}$ | D． | $\frac{b}{{\sqrt{{a^2}+{b^2}}}}$ |
生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二，产生新的微生物（依次被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么标号为1535的微生物会出现在（ ）