题目内容
7．两个相似三角形的面积比为1：4，那么它们的对应中心线的比为1：2．分析 直接根据相似三角形的性质即可得出结论．
解答 解：∵两个相似三角形的面积比为1：4，
∴它们的对应中心线的比为1：2．
故答案为：1：2．
点评 本题考查的是相似三角形的性质，熟知相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比，面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．任意实数a，可用[a]表示不超过a的最大整数，如[4]=4，[$\sqrt{3}$]=1，已知[$\sqrt{n}$]=5，则下列n的值符合条件的是（ ）
| A． | n=5 | B． | n=18 | C． | n=28 | D． | n=36 |
如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F，$\frac{AB}{BC}$=$\frac{2}{3}$，DE=6，则EF=9．
2．
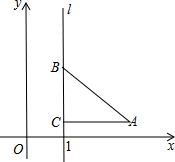如图，直线l是经过点（1，0）且与y轴平行的直线．Rt△ABC中直角边AC=4，BC=3．将BC边在直线l上滑动，使A，B在函数y=$\frac{k}{x}$的图象上．那么k的值是（ ）
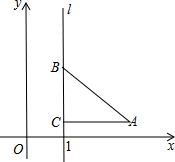如图，直线l是经过点（1，0）且与y轴平行的直线．Rt△ABC中直角边AC=4，BC=3．将BC边在直线l上滑动，使A，B在函数y=$\frac{k}{x}$的图象上．那么k的值是（ ）| A． | 3 | B． | 6 | C． | 12 | D． | $\frac{15}{4}$ |
如图，直线y=$\frac{2}{3}$x-2分别交x轴、y轴于A、B两点，O是原点．
17．小强到体育用品商店购买羽毛球球拍和乒乓球球拍，已知购买1副羽毛球球拍和1副乒乓球球拍共需50元，小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍．若设每副羽毛球拍为x元，每副乒乓球拍为y元，根据题意，下面所列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=50}\\{10（x+y）=320}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |