题目内容
2.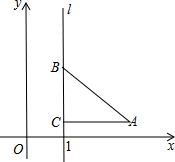 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )| A. | 3 | B. | 6 | C. | 12 | D. | $\frac{15}{4}$ |
分析 过点B作BM⊥y轴于点M,过点A作AN⊥x轴于点N,延长AC交y轴于点D,设点C的坐标为(1,y),根据反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值是个定值作为相等关系求得y值后再求算k值.
解答 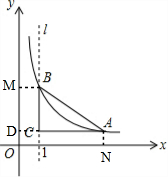 解:过点B作BM⊥y轴、于点M,过点A作AN⊥x轴于点N,延长AC交y轴于点D,设点C的坐标为(1,y),
解:过点B作BM⊥y轴、于点M,过点A作AN⊥x轴于点N,延长AC交y轴于点D,设点C的坐标为(1,y),
∵AC=4,BC=3
∴OM=3+y,ON=5,
∴B(1,3+y),A(5,y),
∴$\left\{\begin{array}{l}3+y=k\\ 5y=k\end{array}\right.$,
∴5y=3+y,
解得,y=$\frac{3}{4}$,
∴OM=3+$\frac{3}{4}$=$\frac{15}{4}$,
∴k=OM×1=$\frac{15}{4}$.
故选D.
点评 此题考查的是反比例函数图象上点的坐标特点,难度稍大,综合性比较强,注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值.

练习册系列答案
相关题目
 如图所示,沿DE折叠矩形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,求CE的长.
如图所示,沿DE折叠矩形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,求CE的长.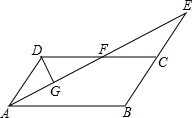 如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F. 如图,点D,E分别是△ABC的BC,AC边的中点,若AB=2,则DE的长1.
如图,点D,E分别是△ABC的BC,AC边的中点,若AB=2,则DE的长1.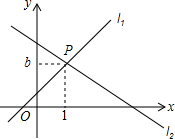 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).