题目内容
 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.求证:AF⊥BF.
考点:三角形中位线定理
专题:证明题
分析:首先根据三角形中位线定理可得DE∥BC,然后再证明AD=DB=DF,再根据等边对等角可得∠DAF=∠DFA,再根据三角形内角和定理可证出∠AFD+∠BFD=90°,进而可得答案.
解答:证明:∵BF平分∠ABC,
∴∠CBF=∠ABF,
∵D、E为AB、AC中点,
∴DE∥BC,AD=DB,
∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=DB,
∴DF=AD,
∴∠DAF=∠DFA,
∵∠DAF+∠DFA+∠DBF+∠DFB=180°,
∴∠AFD+∠BFD=90°,
∴AF⊥BF.
∴∠CBF=∠ABF,
∵D、E为AB、AC中点,
∴DE∥BC,AD=DB,

∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=DB,
∴DF=AD,
∴∠DAF=∠DFA,
∵∠DAF+∠DFA+∠DBF+∠DFB=180°,
∴∠AFD+∠BFD=90°,
∴AF⊥BF.
点评:此题主要考查了三角形中位线定理,以及等边对等角,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(-2)0=0 | ||
| B、3-2=-9 | ||
| C、(a-3)2=a6 | ||
D、a-3=
|
 如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为
如图,已知⊙O的半径R=4,点P是⊙O内的一定点,且OP=2,则过点P的直线与⊙O交于AB,则AB的最小值为 已知如图,∠OAC=36°,AB=BC,求∠AOB的度数.
已知如图,∠OAC=36°,AB=BC,求∠AOB的度数. 在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC.
在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC. 如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.
如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.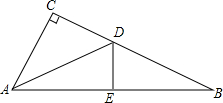 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E. 如图,直线a∥b,∠3=131°,求∠1,∠2的度数.
如图,直线a∥b,∠3=131°,求∠1,∠2的度数.