题目内容
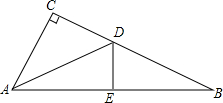 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.(1)若AD=10,sin∠ADC=
| 4 |
| 5 |
(2)如图,若∠B=a,AD=BD=1,则可以利用该图求出sin2a与a的三角函数之间的等量关系(用sina和cosa的值表示).
考点:解直角三角形,线段垂直平分线的性质
专题:计算题
分析:(1)在Rt△ACD中利用∠ADC的正弦即可得到AC=8,再利用勾股定理计算出CD=6,接着根据折叠的性质得DB=DA=10,所以BC=CD+DB=16,然后在Rt△ABC中利用正切的定义求解;
(2)先得到∠ADC=2∠B=2α,由sin∠ADC=
得到AC=sin2α,在Rt△BDE中由cosB=
得到BE=cosα,所以AB=2BE=2cosα,然后在Rt△ABC中利用∠B的正弦即可得到sin2α=2cosα•sinα.
(2)先得到∠ADC=2∠B=2α,由sin∠ADC=
| AC |
| AD |
| BE |
| DB |
解答:解:(1)在Rt△ACD中,∵sin∠ADC=
=
,
而AD=10,
∴AC=8;
∴CD=
=6,
∵AB的垂直平分线与BC,AB的交点分别为D,E,
∴DB=DA=10,
∴BC=CD+DB=16,
在Rt△ABC中,tanB=
=
=
;
(2)∵DA=DB,
∴∠DAB=∠B=α,
∴∠ADC=2∠B=2α,
∵sin∠ADC=
,
∴AC=sin2α,
在Rt△BDE中,∵cosB=
,
∴BE=cosα,
∴AB=2BE=2cosα,
在Rt△ABC中,∵sinB=
,
∴AC=ABsinB,
∴sin2α=2cosα•sinα.
| AC |
| AD |
| 4 |
| 5 |
而AD=10,
∴AC=8;
∴CD=
| AD2-AC2 |
∵AB的垂直平分线与BC,AB的交点分别为D,E,
∴DB=DA=10,
∴BC=CD+DB=16,
在Rt△ABC中,tanB=
| AC |
| BC |
| 8 |
| 16 |
| 1 |
| 2 |
(2)∵DA=DB,
∴∠DAB=∠B=α,
∴∠ADC=2∠B=2α,
∵sin∠ADC=
| AC |
| AD |
∴AC=sin2α,
在Rt△BDE中,∵cosB=
| BE |
| DB |
∴BE=cosα,
∴AB=2BE=2cosα,
在Rt△ABC中,∵sinB=
| AC |
| AB |
∴AC=ABsinB,
∴sin2α=2cosα•sinα.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了线段的垂直平分线.

练习册系列答案
相关题目
已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是( )
| A、直角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
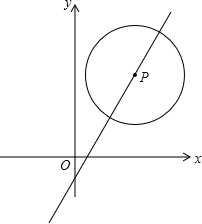 如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知半径为2的⊙P圆心P在直线y=2x-1的图象上运动. 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.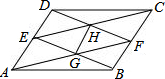 在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.
在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC. 已知:∠A=∠B,求证:∠C=∠D.
已知:∠A=∠B,求证:∠C=∠D. 已知:如图,E点为DF上的点,B为AC上的点,∠EHF=∠AGB,∠C=∠D.
已知:如图,E点为DF上的点,B为AC上的点,∠EHF=∠AGB,∠C=∠D.