题目内容
 在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC.
在?ABCD中,E,F分别是AB,BC上的点,且AF=CE,设AF与CE相交于点G,求证:∠DGA=∠DGC.考点:平行四边形的性质
专题:证明题
分析:过D作DQ⊥AF,DH⊥CE,并连接DE和DF,利用等积法求得两条垂线段相等,从而利用角平分线的判定定理证得结论即可.
解答: 证明:过D作DQ⊥AF,DH⊥CE,并连接DE和DF,如右图所示:
证明:过D作DQ⊥AF,DH⊥CE,并连接DE和DF,如右图所示:
则S△ADF=
S平行四边形ABCD=S△DEC,
∴
AF•DQ=
DH•EC,
又∵AF=EC,
∴DQ=DH,
∴GD为∠AGC的角平分线,
∴∠DGA=∠DGC(角平分线逆定理).
 证明:过D作DQ⊥AF,DH⊥CE,并连接DE和DF,如右图所示:
证明:过D作DQ⊥AF,DH⊥CE,并连接DE和DF,如右图所示:则S△ADF=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
又∵AF=EC,
∴DQ=DH,
∴GD为∠AGC的角平分线,
∴∠DGA=∠DGC(角平分线逆定理).
点评:本题考查平行四边形和角平分线的性质,有一定难度,解题关键是准确作出辅助线,利用角平分线的性质进行证明.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
 如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.
如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.| A、0 | B、1 | C、2 | D、3 |
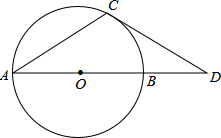 如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30°
如图,点D在⊙O的直径AB的延长线上,点C在⊙C上,AC=CD,∠D=30° 如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点.
如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、C分别在x轴的负半轴、y轴的正半轴上,已知A(-1,0)、D(2,3),并且二次函数y=ax2+bx+c的图象经过A、C、D三点. 如图,已知四边形ABCD中,∠A=106°-α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2.
如图,已知四边形ABCD中,∠A=106°-α,∠ABC=74°+α,BD⊥DC于D,EF⊥DC于F,求证:∠1=∠2. 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.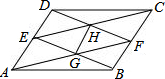 在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.
在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.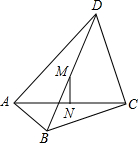 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=6,CD=AC=8,M、N分别是对角线BD、AC的中点.