题目内容
 如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.
如图所示,在平行四边形ABCD中,点E,F分别在AD,BC上,且BE∥DF,AC与EF相交于点O.证明:O为AC,EF的中点.考点:平行四边形的性质
专题:证明题
分析:连接AF、CE,证明四边形AECF为平行四边形即可得到AC、EF互相平分.
解答: 证明:连接AF、CE,
证明:连接AF、CE,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD﹦BC,
又∵DF∥BE,
∴四边形EBFD是平行四边形,
∴BE=DF,DE=BF,
∴AE﹦CF,
又∵AF∥CE,
∴四边形AECF为平行四边形,
∴AC、EF互相平分,
即:O为AC,EF的中点.
 证明:连接AF、CE,
证明:连接AF、CE,∵四边形ABCD为平行四边形,
∴AD∥BC,AD﹦BC,
又∵DF∥BE,
∴四边形EBFD是平行四边形,
∴BE=DF,DE=BF,
∴AE﹦CF,
又∵AF∥CE,
∴四边形AECF为平行四边形,
∴AC、EF互相平分,
即:O为AC,EF的中点.
点评:本题考查了平行四边形的性质和判定,是中考常见题型,比较简单,解题的关键是正确的构造辅助线.

练习册系列答案
相关题目
 如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=35°,则∠AOC的度数为( )| A、20° | B、40° |
| C、60° | D、70° |
 如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.
如图,在直线MN上找点P,使点P到∠AOB两边的距离相等,符合条件的有( )个.| A、0 | B、1 | C、2 | D、3 |
已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是( )
| A、直角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
下列命题错误的是( )
A、若a<0,则
| ||||||
| B、如果一组数据16,19,19,x的平均数比众数小1,那么这组数据的中位数是18.5 | ||||||
C、已知函数y=
| ||||||
| D、若关于x的一元二次方程(m-2)x2+3x=4-m2有一个根是0,则m=±2 |
 如图,已知AD∥BC,M为AB的中点.
如图,已知AD∥BC,M为AB的中点. 在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.
在△ABC中,D、E为AB、AC中点,DE与∠B的平分线交于F,如图所示.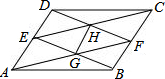 在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.
在平行四边形ABCD中,E,F分别在AD,BC上,且AE=BF,AF,BE交于G,EC,FD交于H,求证:GH∥BC.