题目内容
1．已知：5a=4，5b=6，5c=9，（1）求52a-b的值；
（2）试说明：2b=a+c．
分析 （1）根据幂的运算将52a-b=（5a）2÷5b，再代入求值即可；
（2）分别计算出5a+c、52b的值，即可得a+c=2b．
解答 解：（1）当5a=4，5b=6时，
52a-b=52a÷5b=（5a）2÷5b=42÷6=$\frac{8}{3}$；
（2）∵5a+c=5a×5c=4×9=36，52b=62=36，
∴5a+c=52b，
故a+c=2b．
点评 本题主要考查幂的运算，熟悉幂的四则运算法则是基本，根据不同题目对法则的灵活运用是关键．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
如图，线段AB是半径为6的⊙O的直径，点C是弧AB的中点，点M、N在线段AB上（AM＜BN），MN=5．若∠MCN=45°，线段AM的长度为3或4．
12．已知A、B两地相距630千米，在A、B之间有汽车站C站，如图1所示．客车由A地驶向C站、货车由B地驶向A地，两车同时出发，匀速行驶，货车的速度是客车速度的$\frac{3}{4}$．图2是客、货车离C站的路程y1、y2（千米）与行驶时间x（小时）之间的函数关系图象．则下列说法不正确的是（ ）
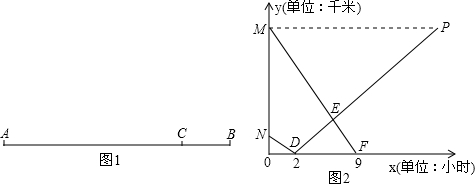
| A． | 货车行驶2小时到达C站 | B． | 货车行驶完全程用时14小时 | ||
| C． | 图2中的点E的坐标是（7，180） | D． | 客车的速度是60千米∕时 |
如图，△ABC中，EF∥BC，ED∥AB，FG∥AC，AF：FB=1：2，S△ABC=18，则图中阴影部分的面积为（ ）
13．下列计算中，正确的是（ ）
| A． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B． | $\sqrt{8}+\sqrt{2}=\sqrt{10}$ | C． | $\sqrt{8}÷\sqrt{2}=4$ | D． | $\sqrt{8}×\sqrt{2}=4$ |
11．已知A，B，C三个数，其中A=-$\frac{\sqrt{2}}{2}$，B=0，C=-$\frac{1}{\sqrt{3}}$，则A，B，C的大小关系是（ ）
| A． | C＞A＞B | B． | B＞A＞C | C． | C＞B＞A | D． | B＞C＞A |