题目内容
12.已知A、B两地相距630千米,在A、B之间有汽车站C站,如图1所示.客车由A地驶向C站、货车由B地驶向A地,两车同时出发,匀速行驶,货车的速度是客车速度的$\frac{3}{4}$.图2是客、货车离C站的路程y1、y2(千米)与行驶时间x(小时)之间的函数关系图象.则下列说法不正确的是( )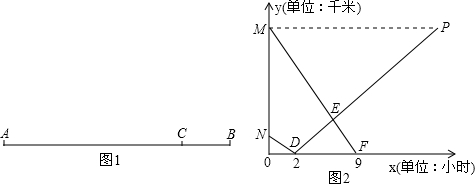
| A. | 货车行驶2小时到达C站 | B. | 货车行驶完全程用时14小时 | ||
| C. | 图2中的点E的坐标是(7,180) | D. | 客车的速度是60千米∕时 |
分析 根据图象中点D的实际意义可判断A选项;客车的速度为a km/h、货车的速度为$\frac{3}{4}$akm/h,根据客车9小时到达C地、货车2小时到达C地列出方程可得客车、货车速度从而判断B、D选项;根据点E的实际意义两车相遇,可列方程:45x+60x=630解方程可得点E的坐标.
解答 解:A、由图可知当x=2时,y2=0,表示火车行驶2小时到达C站,故选此选项正确;
B、设客车的速度为a km/h,则货车的速度为$\frac{3}{4}$akm/h,由题意列方程得:
9a+$\frac{3}{4}$a×2=630,解得:a=60,∴$\frac{3}{4}$a=45,
即客车的速度为60 km/h,货车的速度为45km/h,
则货车行驶完全程用时为630÷45=14小时,故此选项正确;
C、点E表示两车离C站路程相同,结合题意,两车相遇,
可列方程:45x+60x=630,解得:x=6,
∴540-60x=180,∴E (6,180)
故此选项错误;
D、由B选项可知客车的速度为60 km/h,故此选项正确;
故选:C.
点评 本题考查了一次函数的应用及一元一次方程的应用,解题的关键是根据题意结合图象说出其图象表示的实际意义,这样便于理解题意及正确的解题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
3. 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )| A. | n可以为3和4 | |
| B. | n可以为所有正偶数 | |
| C. | n可以为所有大于2的整数 | |
| D. | 正整数中所有3的倍数的数都可以为n值 |
20.已知线段AB=6cm,点C是直线AB上一点,BC=4cm,则线段AC的长度是( )
| A. | 10cm | B. | 2cm | C. | 2cm或10cm | D. | 5cm |
4.下列轴对称图形中,有3条对称轴的图形是( )
| A. | 角 | B. | 正方形 | C. | 等边三角形 | D. | 等腰直角三角形 |
 如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.
如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.