题目内容
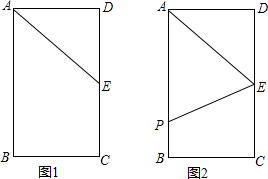
9. 如图,△ABC中,EF∥BC,ED∥AB,FG∥AC,AF:FB=1:2,S△ABC=18,则图中阴影部分的面积为( )
如图,△ABC中,EF∥BC,ED∥AB,FG∥AC,AF:FB=1:2,S△ABC=18,则图中阴影部分的面积为( )| A. | 2 | B. | 4 | C. | 4.5 | D. | 9 |
分析 根据平行四边形的判定与性质得出EF=BD=GC,进而得出BD=DG=GC,即可得出S△AEF=S△FEH=S△DGH,求出答案即可.
解答  解:∵EF∥BC,ED∥AB,FG∥AC,
解:∵EF∥BC,ED∥AB,FG∥AC,
∴四边形FBDE和四边形FGCE都是平行四边形,
∴EF=BD=GC,
∵AF:FB=1:2,
∴$\frac{AF}{AB}$=$\frac{1}{3}$,
∴BD=DG=GC,
∵EF∥BC,
∴△FHE∽△DGH,
∵EF=DG,
∴△FHE≌△DGH,
故可得S△AEF=S△FEH=S△DGH,
∴EF∥BC,
∴△AFE∽△ABC,
∵$\frac{AF}{AB}$=$\frac{1}{3}$,
∴$\frac{{S}_{△AFE}}{{S}_{△ABC}}$=$\frac{1}{9}$,
∵S△ABC=18,
∴S△AFE=2,
∴图中阴影部分的面积为4.
故选:B.
点评 此题主要考查了相似三角形的判定与性质,得出S△AEF=S△FEH=S△DGH是解题关键.

练习册系列答案
相关题目
20.已知线段AB=6cm,点C是直线AB上一点,BC=4cm,则线段AC的长度是( )
| A. | 10cm | B. | 2cm | C. | 2cm或10cm | D. | 5cm |
4.下列轴对称图形中,有3条对称轴的图形是( )
| A. | 角 | B. | 正方形 | C. | 等边三角形 | D. | 等腰直角三角形 |
18.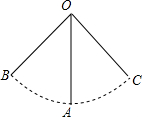 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
 某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )
某新建小区里安装了一架秋千,如图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是( )| A. | 3$\sqrt{2}$米 | B. | $\frac{3\sqrt{2}}{2}$米 | C. | $\frac{6-3\sqrt{2}}{2}$米 | D. | 无法确定 |
19.当a=-2时,下列运算中,错误的是( )
| A. | $\frac{1}{a}$•a=1 | B. | |a-2|+|a+1|=5 | C. | -a3+a+(-a)2=10 | D. | $\frac{1}{a}$-$\frac{1}{{a}^{2}}$=$\frac{1}{4}$ |
 如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.
如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.